要通过数值方法求解偏微分方程，可以先将求解区域划分成细密的网格，然后在时间域上迭代更新。

1. 问题描述

在给定初值条件的情况下，通过数值方法近似求解波动方程:

\[\frac{\partial ^2u}{\partial t^2}=\Delta u=\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2}\]

在下文中，我们将 $u(x,y,z,t)$ 简记为 $u(\mathbf{x},t)$.

1.1. 问题区域

我们先将问题区域限定在一个立方体中:

\[\Omega=\left[0 \leqslant x \leqslant L_{x}\right] \times\left[0 \leqslant y \leqslant L_{y}\right] \times\left[0 \leqslant z \leqslant L_{z}\right]\]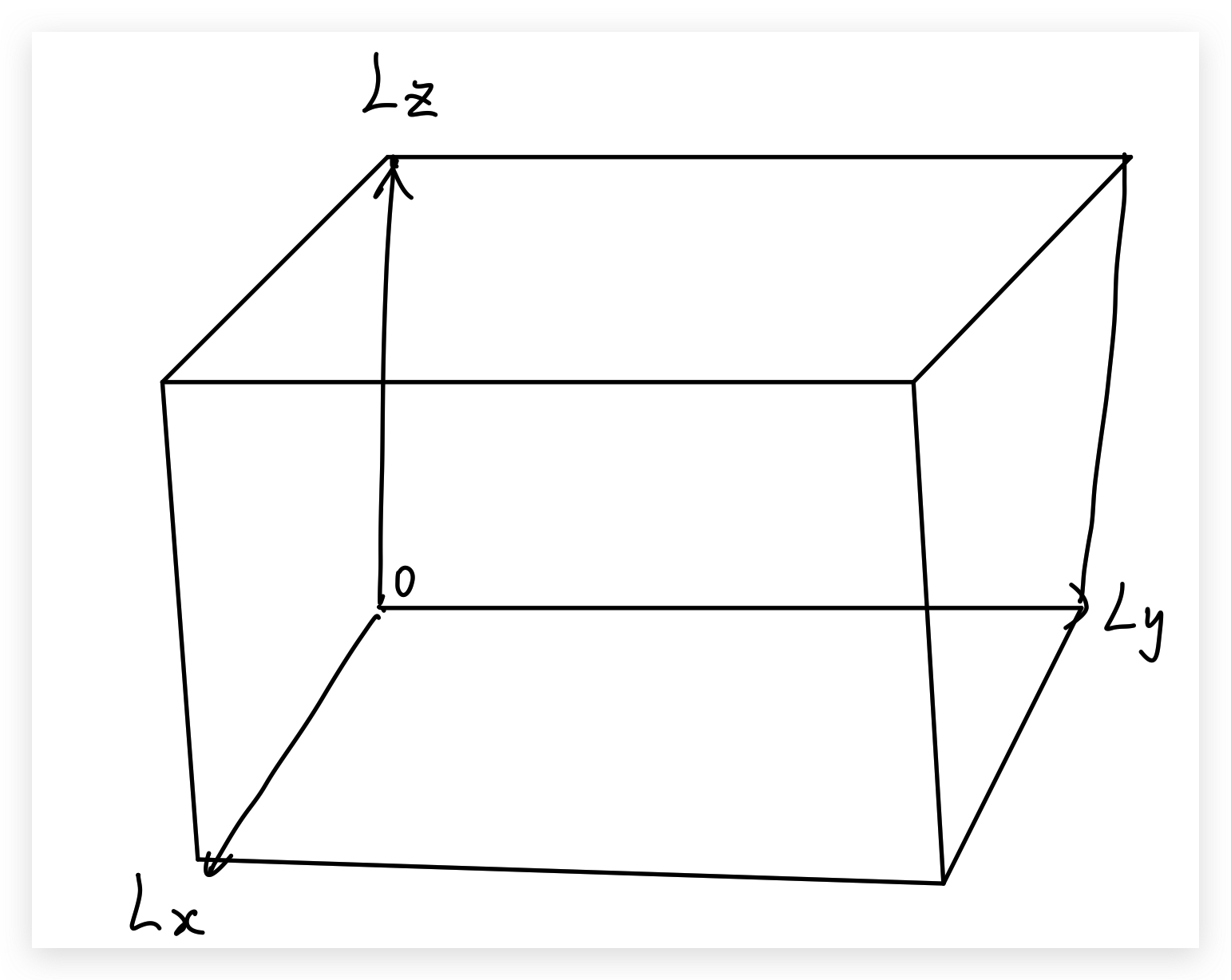

问题区域

1.2. 初值条件

首先是时间上的初值条件：

\[\begin{aligned} \left.u\right|_{t=0} &=\varphi(x, y, z) \\ \left.\frac{\partial u}{\partial t}\right|_{t=0} &=0 \end{aligned}\]

然后是空间上的初值条件，可以有两种情况：第一类齐次边界条件，也就是在边界上都为0，

\[\begin{array}{ll} u(0, y, z, t)=0, & u\left(L_{x}, y, z, t\right)=0 \\ u(x, 0, z, t)=0, & u\left(x, L_{y}, z, t\right)=0 \\ u(x, y, 0, t)=0, & u\left(x, y, L_{z}, t\right)=0 \end{array}\]

或周期性边界条件，

\[\begin{array}{ll} u(0, y, z, t)=u\left(L_{x}, y, z, t\right), & u_{x}(0, y, z, t)=u_{x}\left(L_{x}, y, z, t\right) \\ u(x, 0, z, t)=u\left(x, L_{y}, z, t\right), & u_{y}(x, 0, z, t)=u_{y}\left(x, L_{y}, z, t\right) \\ u(x, y, 0, t)=u\left(x, y, L_{z}, t\right), & u_{z}(x, y, 0, t)=u_{z}\left(x, y, L_{z}, t\right) \end{array}\]

2. 数值求解

2.1. 差分法

所谓差分就是用数值的方法来近似计算梯度:

\[\begin{aligned} \frac{\partial f(x)}{\partial x}&= \lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\\ &\approx \frac{f(x+\Delta x)-f(x)}{\Delta x} \\ \end{aligned}\] \[\begin{aligned} \dfrac{\partial ^{2}f}{\partial x^{2}} &= \lim_{\Delta x\rightarrow 0} \frac{f'(x+\Delta x)-f'(x)}{\Delta x}\\ &\approx \frac{\frac{f\left( x+\Delta x\right) -f\left( x\right) }{\Delta x}-\frac{f\left( x\right) -f\left( x-\Delta x\right) }{\Delta x}}{\Delta x}\\ &= \frac{f(x+\Delta x)+f(x-\Delta x)-2f(x)}{\Delta x^2}\\ \end{aligned}\]

2.2. 网格划分

我们将立方体区域 $\Omega$ 划分为 $N\times N \times N$的立方体网格，每个网格的尺寸为 $h_x\times h_y \times h_z$. 我们以每个网格的顶点作为计算节点，如下图所示.

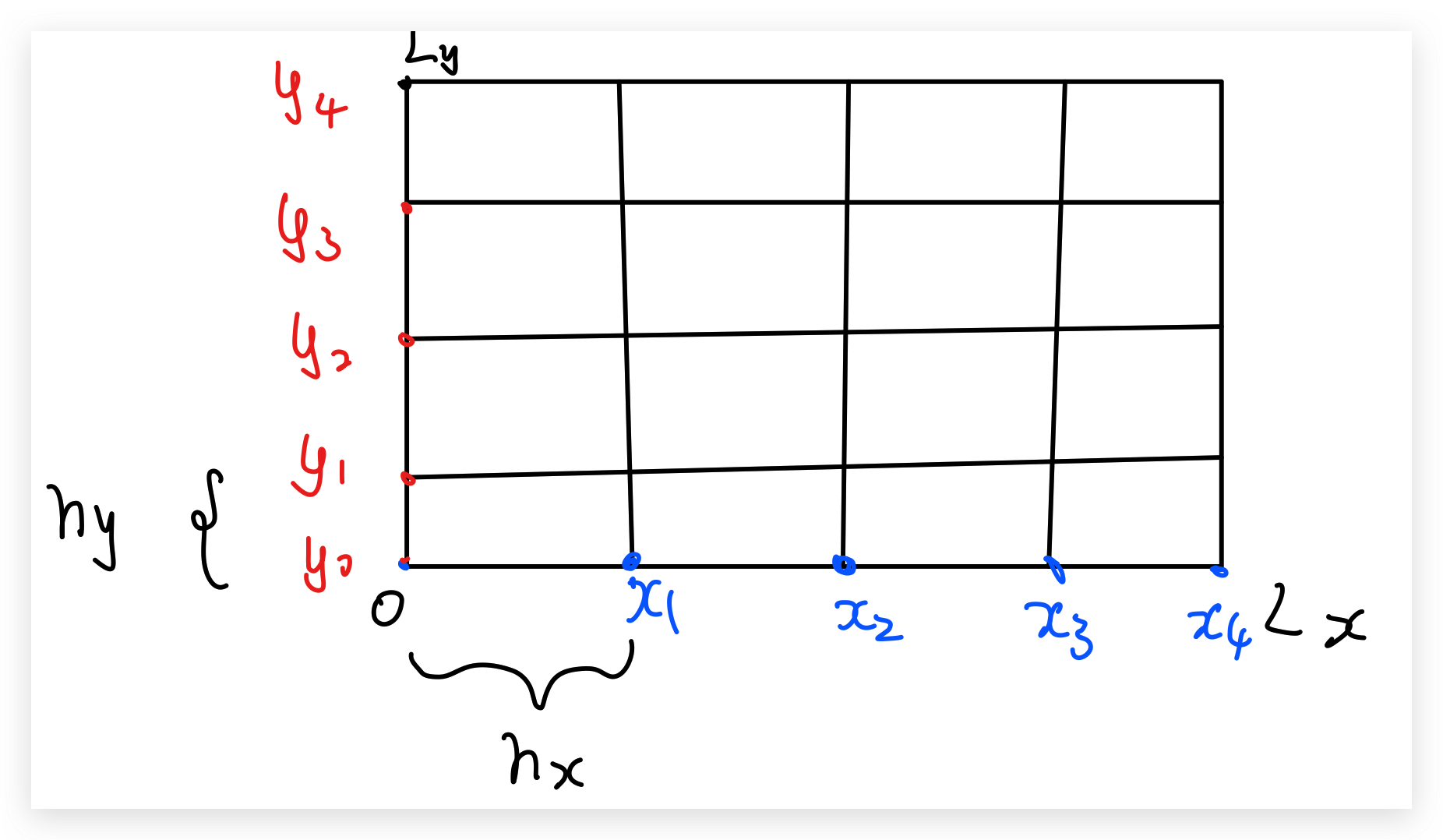
以$N=4$的二维情况为例

\[\begin{aligned} \bar{\omega}_{h} &=\left\{\left(x_{i}=i h_{x}, y_{j}=j h_{y}, z_{k}=k h_{z}\right), i, j, k=0,1, \ldots, N, h_{x} N=L_{x}, h_{y} N=L_{y}, h_{z} N=L_{z}\right\} \\ \omega_{\tau} &=\left\{t_{n}=n \tau, n=0,1, \ldots, K, \tau K=T\right\}. \end{aligned}\]

上面的公式中， \(\bar{\omega}_{h}\) 表示网格区域的划分，\(\omega_{\tau}\) 表示时间上的划分，每个时间节点之间的跨度为 $\tau$.

2.3. 差分模拟

我们要通过数值近似模拟波动方程：

\[\frac{\partial ^2u}{\partial t^2}=\Delta u=\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2}\]

首先将函数 $u(x,y,z,t)$ 在节点$(x_i,y_j,z_k,t_n)$处取值，记为：

\[u(x_i,y_j,z_k,t_n)=u_{ijk}^n\]

这里的下标 $i,j,k$ 表示在空间上的$(x_i,y_j,z_k)$处取值，上标 $n$ 表示此时的时间为$t_n$.

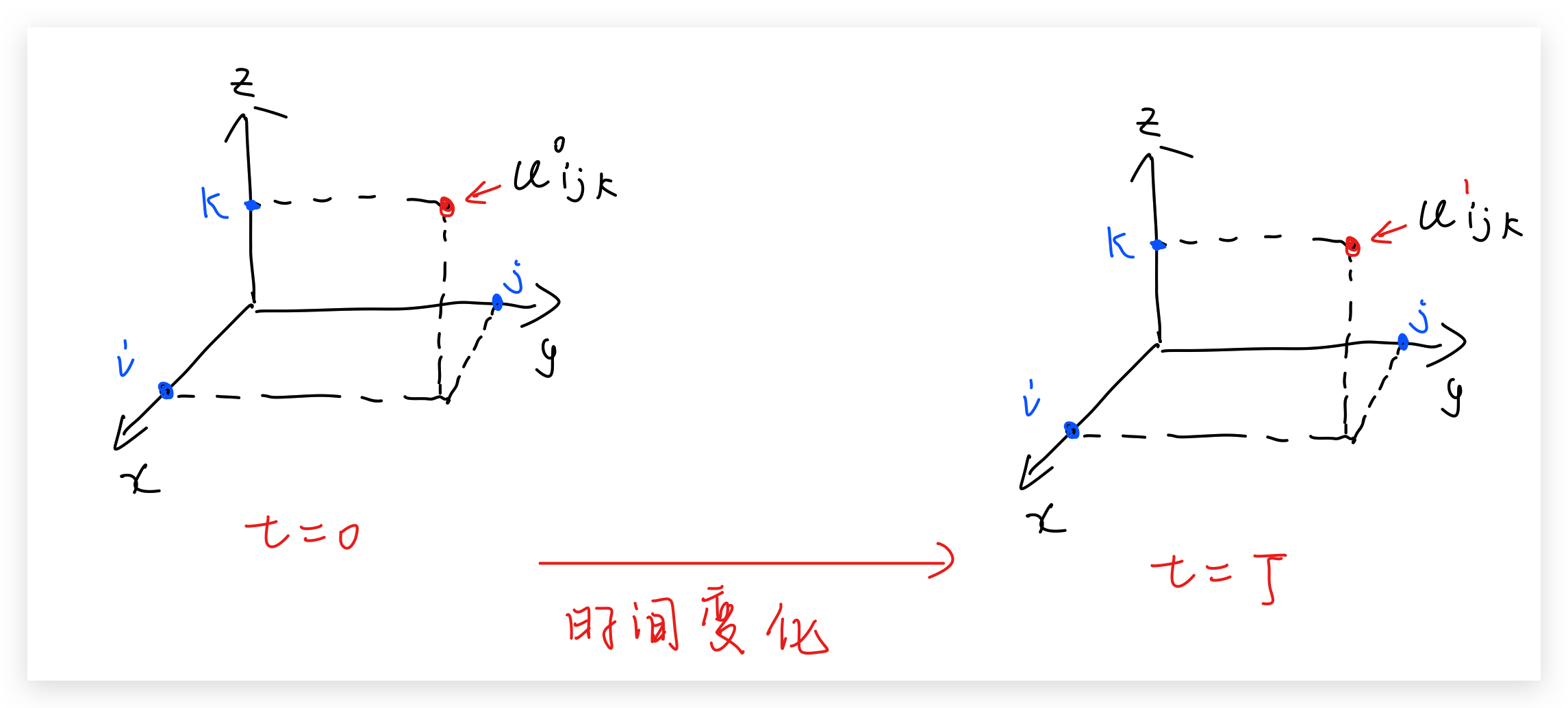
$u_{ijk}^n$

2.3.1. 等式左侧的模拟

我们先对等式左侧进行差分模拟:

\[\frac{\partial ^2u(\mathbf{x},t)}{\partial t^2}\approx \frac{u(\mathbf{x},t+\Delta t)+u(\mathbf{x},t-\Delta t)-2u(\mathbf{x},t)}{\Delta t^2}\]

体现在网格上就是：

\[\frac{\partial ^2u(\mathbf{x},t_n)}{\partial t^2}\approx \frac{u(\mathbf{x},t_{n+1})+u(\mathbf{x},t_{n-1})-2u(\mathbf{x},t_{n})}{\tau^2}\]

简写为上下标的形式为：

\[\left. \dfrac{\partial ^2u(\mathbf{x},t)}{\partial t^2} \right |_{u_{i j k}^{n}} \approx \dfrac{u_{i j k}^{n+1}-2 u_{i j k}^{n}+u_{i j k}^{n-1}}{\tau^{2}}\]

2.3.2. 等式右侧的模拟

接下来是对等式右侧$\Delta u=\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}+\frac{\partial ^2u}{\partial z^2}$的模拟，我们首先模拟 $\frac{\partial ^2u}{\partial x^2}$ :

\[\frac{\partial ^2u(x,y,z,t)}{\partial x^2} \approx \dfrac{u(x+\Delta x,y,z,t)+u(x-\Delta x,y,z,t)-2u(x,y,z,t)}{\Delta x^2}\]

即：

\[\left. \dfrac{\partial ^2u}{\partial x^2} \right |_{u_{i j k}^{n}} \approx \dfrac{u_{i+1, j, k}^{n}-2 u_{i, j, k}^{n}+u_{i-1, j, k}^{n}}{h_x^{2}}\]

类似的，我们可以求出$u$关于$y$和$z$的二阶导，整合后得到：

\[\Delta {u_{i j k}^{n}} \approx \dfrac{u_{i+1, j, k}^{n}-2 u_{i, j, k}^{n}+u_{i-1, j, k}^{n}}{h_x^{2}} + \dfrac{u_{i, j+1, k}^{n}-2 u_{i, j, k}^{n}+u_{i, j-1, k}^{n}}{h_y^{2}} + \dfrac{u_{i, j, k+1}^{n}-2 u_{i, j, k}^{n}+u_{i, j, k-1}^{n}}{h_z^{2}}\]

2.4. 迭代求解

我们通过波动方程的离散形式：

\[\left. \dfrac{\partial ^2u(\mathbf{x},t)}{\partial t^2} \right |_{u_{i j k}^{n}}= \Delta {u_{i j k}^{n}}\]

获得了方程组：

\[\dfrac{u_{i j k}^{n+1}-2 u_{i j k}^{n}+u_{i j k}^{n-1}}{\tau^{2}}=\dfrac{u_{i+1, j, k}^{n}-2 u_{i, j, k}^{n}+u_{i-1, j, k}^{n}}{h_x^{2}} + \dfrac{u_{i, j+1, k}^{n}-2 u_{i, j, k}^{n}+u_{i, j-1, k}^{n}}{h_y^{2}} + \dfrac{u_{i, j, k+1}^{n}-2 u_{i, j, k}^{n}+u_{i, j, k-1}^{n}}{h_z^{2}}\]

接下来我们对该方程组进行恒定变形，得到：

\[\begin{aligned} u_{i j k}^{n+1}&=2\left( 1-\frac{\tau^{2}}{h_x^{2}}-\frac{\tau^{2}}{h_y^{2}}-\frac{\tau^{2}}{h_z^{2}} \right) u_{i j k}^{n}-u_{i j k}^{n-1} +\frac{\tau^{2}}{h_x^{2}}\left( u_{i+1, j, k}^{n}+u_{i-1, j, k}^{n} \right)\\ &\qquad +\frac{\tau^{2}}{h_y^{2}}\left( u_{i, j+1, k}^{n}+u_{i, j-1, k}^{n} \right) +\frac{\tau^{2}}{h_z^{2}}\left( u_{i, j, k+1}^{n}+u_{i, j, k-1}^{n} \right) \\ & = 2\left( 1-r_x-r_y-r_z \right) u_{i j k}^{n}-u_{i j k}^{n-1} +r_x\left( u_{i+1, j, k}^{n}+u_{i-1, j, k}^{n} \right)\\ &\qquad+r_y\left( u_{i, j+1, k}^{n}+u_{i, j-1, k}^{n} \right) +r_z\left( u_{i, j, k+1}^{n}+u_{i, j, k-1}^{n} \right) \end{aligned}\]

这里将 $\frac{\tau^{2}}{h_x^{2}}$ 记为 $r_x$，使得看起来更简洁。那么我们的迭代策略也很明显了：

\[u_{i j k}^{n+1} =2\left( 1-r_x-r_y-r_z \right) u_{i j k}^{n}-u_{i j k}^{n-1} +r_x\left( u_{i+1, j, k}^{n}+u_{i-1, j, k}^{n} \right)+r_y\left( u_{i, j+1, k}^{n}+u_{i, j-1, k}^{n} \right) +r_z\left( u_{i, j, k+1}^{n}+u_{i, j, k-1}^{n} \right)\]

2.5. 具体流程

  1. 通过 $t=0$ 时的初值条件计算 $u_{ijk}^0=\varphi(x_i,y_j,z_k)$.

  2. 要计算 $u_{ijk}^1$，如果通过上面的方程来计算的话，也就是$n=0$的情况，此时需要 $u^0$ 和 $u^{-1}$，但我们不知道$u^{-1}$的值，这时就需要进行一点修改，原方程为:

    \[\frac{u^{1}-2u^0+u^{-1}}{\tau^2}=\Delta u^0\]

    我们可以假设 $u^{1}-u^0=u^0-u^{-1}$，这样就得到了：

    \[\begin{aligned} u^1_{ijk}&=u^0_{ijk}+\frac{\tau^2}{2}\Delta u^0_{ijk}\\ &=u^0_{ijk}+\frac{\tau^2}{2}\Delta \varphi(x_i,y_j,z_k)\\ \end{aligned}\]

  3. 接下来要计算$u_{ijk}^1,u_{ijk}^2,\ldots$，就可直接用迭代方程求解即可：

\[u_{i j k}^{n+1} =2\left( 1-r_x-r_y-r_z \right) u_{i j k}^{n}-u_{i j k}^{n-1} +r_x\left( u_{i+1, j, k}^{n}+u_{i-1, j, k}^{n} \right)+r_y\left( u_{i, j+1, k}^{n}+u_{i, j-1, k}^{n} \right) +r_z\left( u_{i, j, k+1}^{n}+u_{i, j, k-1}^{n} \right)\]

3. 实验

接下来用 Python 对二维情况进行模拟，这里使用二维情况是为了方便可视化，实际上二维和三维的区别不大。 这里我们对以下函数进行模拟：

\[u(x,y,t)=\sin \left(\frac{\pi}{L_{x}} x\right) \cdot \sin \left(\frac{\pi}{L_{y}} y\right) \cdot \cos \left(a_{t} \cdot t\right),\quad a_{t}=\pi \sqrt{\frac{1}{L_{x}^{2}}+\frac{1}{L_{y}^{2}}}\]

那么我们的初值函数为：

\[\varphi(x,y)=\sin \left(\frac{\pi}{L_{x}} x\right) \cdot \sin \left(\frac{\pi}{L_{y}} y\right)\]

第一步是计算 $u^0$ 的情况： \(u(x_i,y_j,t=0)=\varphi(x_i,y_j)\)

第二步是计算 $u^1$，使用公式：

\[u^1=u^0+\frac{\tau^2}{2}\Delta \varphi(x_i,y_j)\\\]

这里初值函数的Laplace算子为：

\[\Delta \varphi(x,y)=-\left(\left(\frac{\pi}{L_{x}}\right)^2+\left(\frac{\pi}{L_{y}} \right)^2\right)\sin \left(\frac{\pi}{L_{x}} x\right) \cdot \sin \left(\frac{\pi}{L_{y}} y\right)\]

第三步为迭代更新：

\[u_{i j}^{n+1} =2\left( 1-r_x-r_y \right) u_{i j }^{n}-u_{i j }^{n-1} +r_x\left( u_{i+1, j}^{n}+u_{i-1, j}^{n} \right) +r_y\left( u_{i, j+1}^{n}+u_{i, j-1}^{n} \right)\]

这里我们有一点要注意：我们更新 $u^{n+1}_{ij}$ 时需要用到上下左右中 5 个顶点的值来计算差分，但边界上的 $u$ 值可以直接根据边界条件算出，不需要通过差分模拟计算，这也就避免了边界点处无法计算差分的问题。

在输入条件为 $L_x=L_y=2,T=4,N=50,K=500$ 的情况下，我们得到的模拟解大致是这样的：

wave

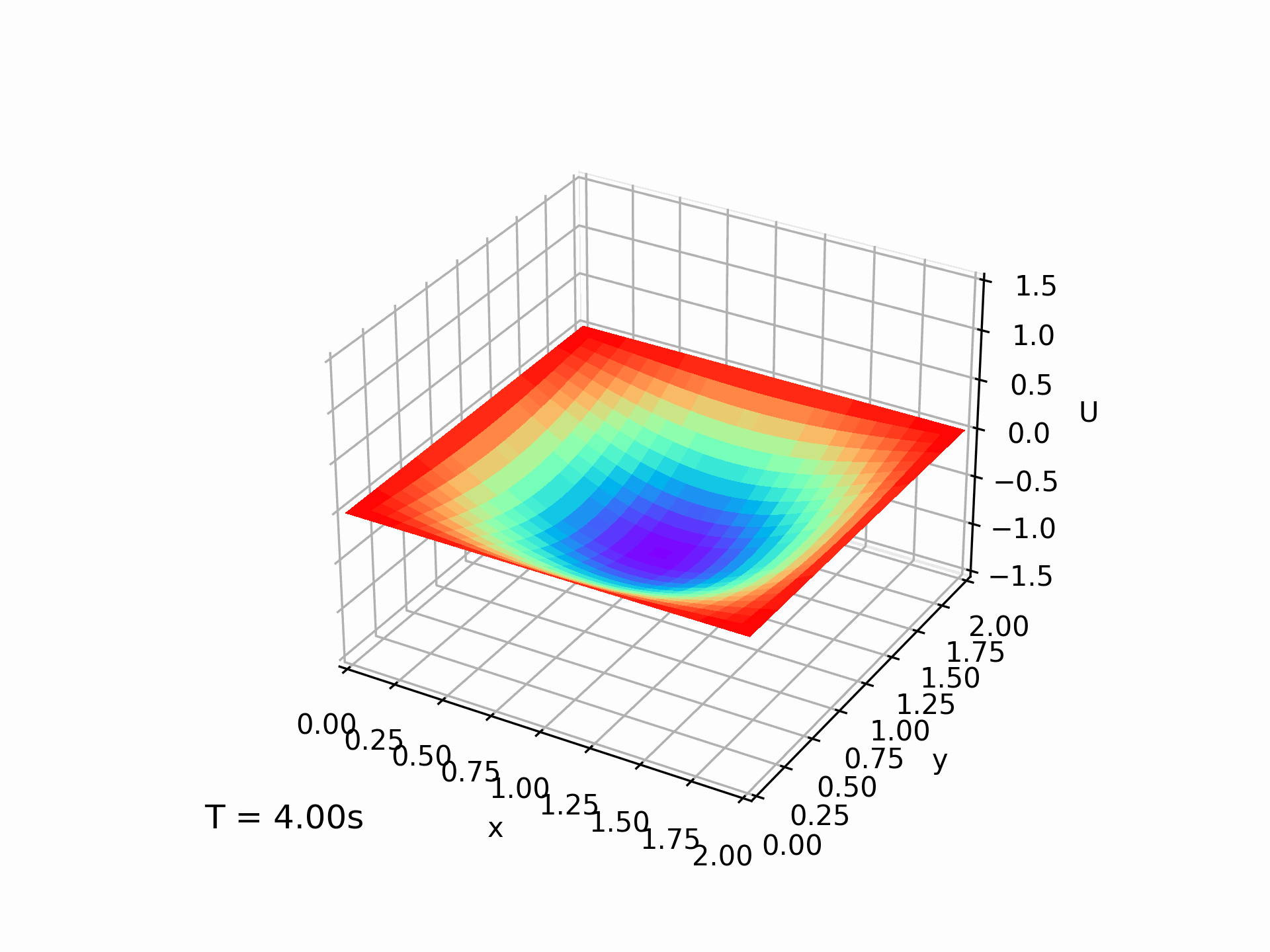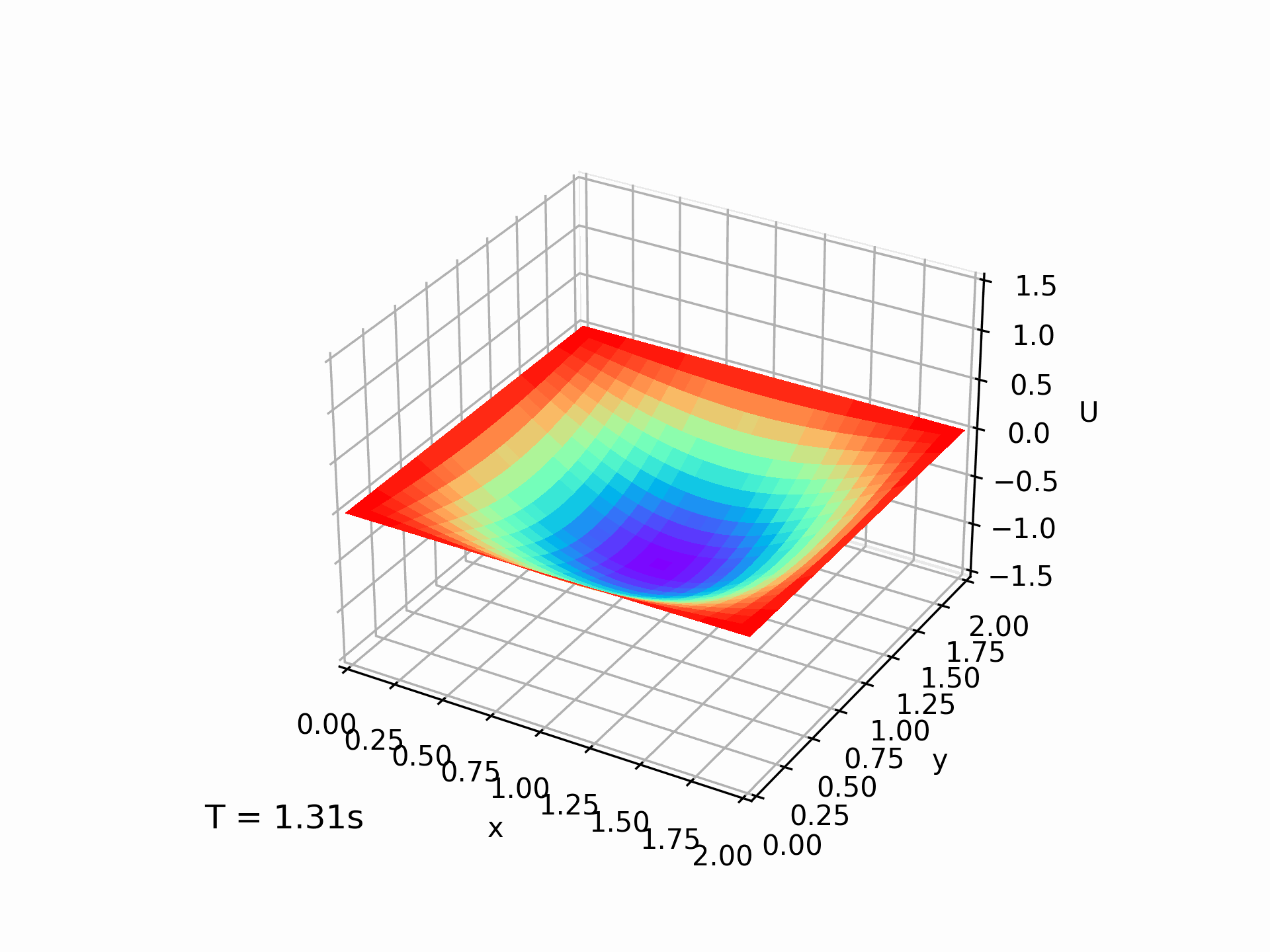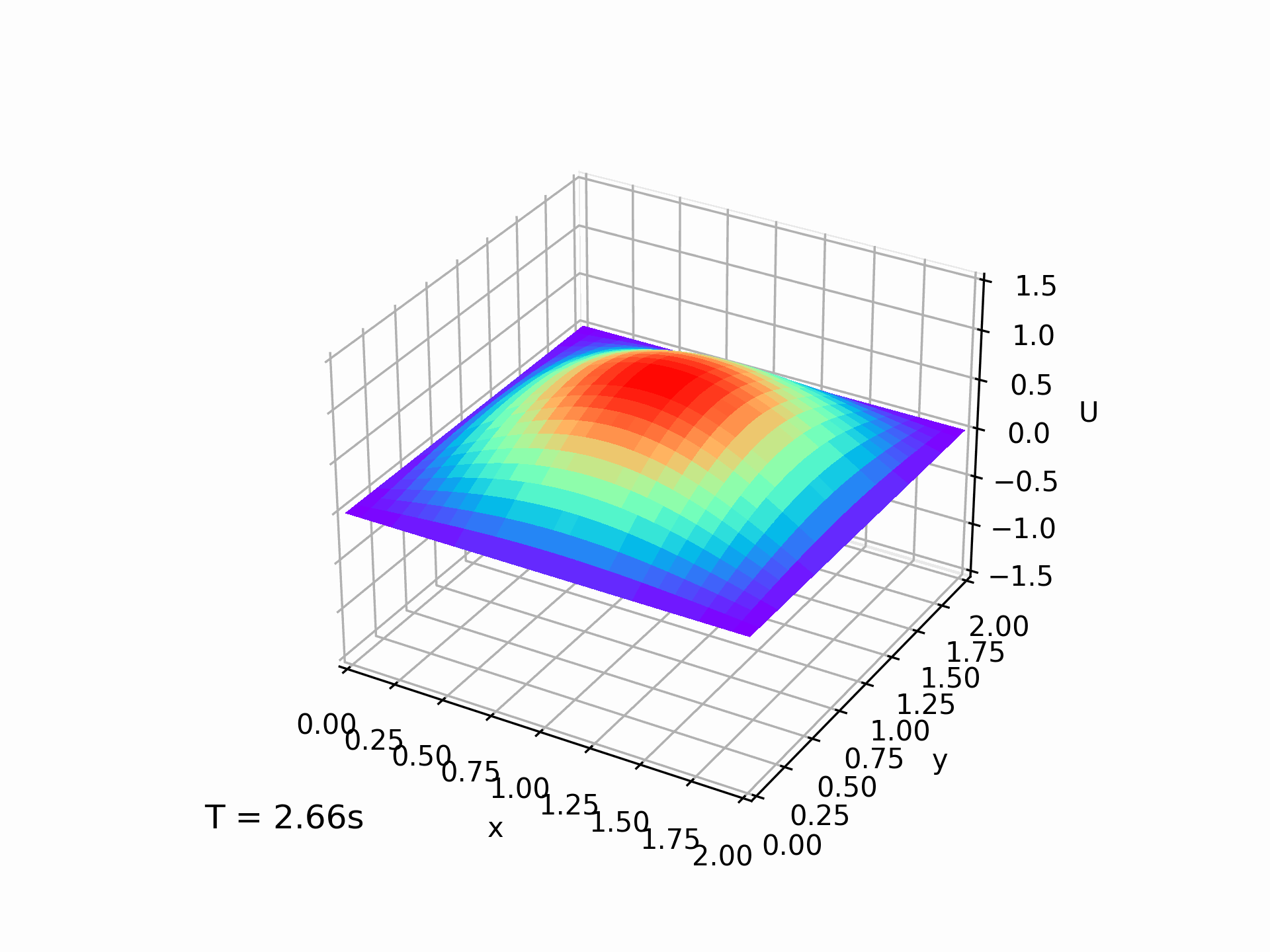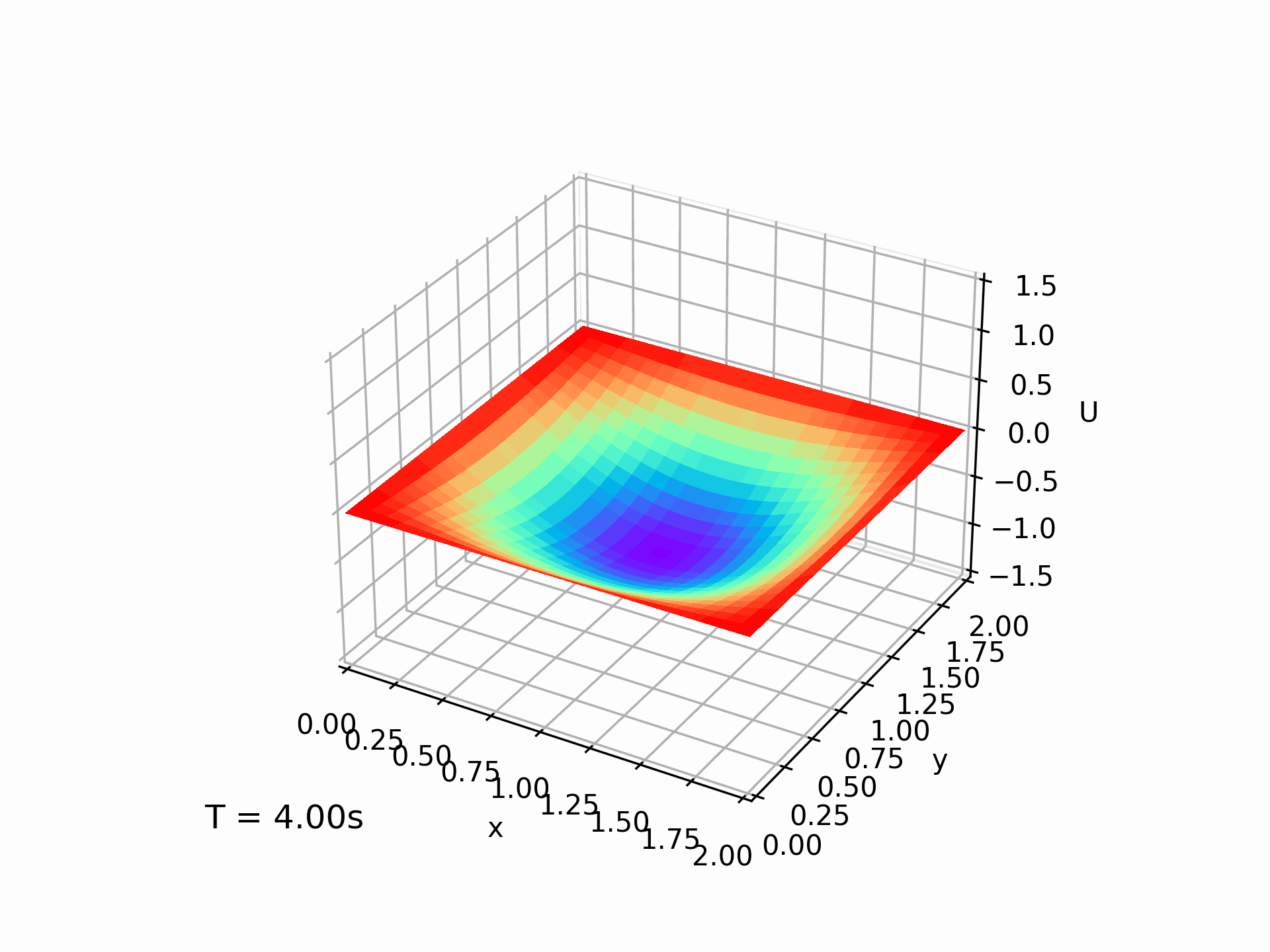
我们也计算了误差随着迭代次数的变化情况，居然还能忽上忽下，属实有点神奇。

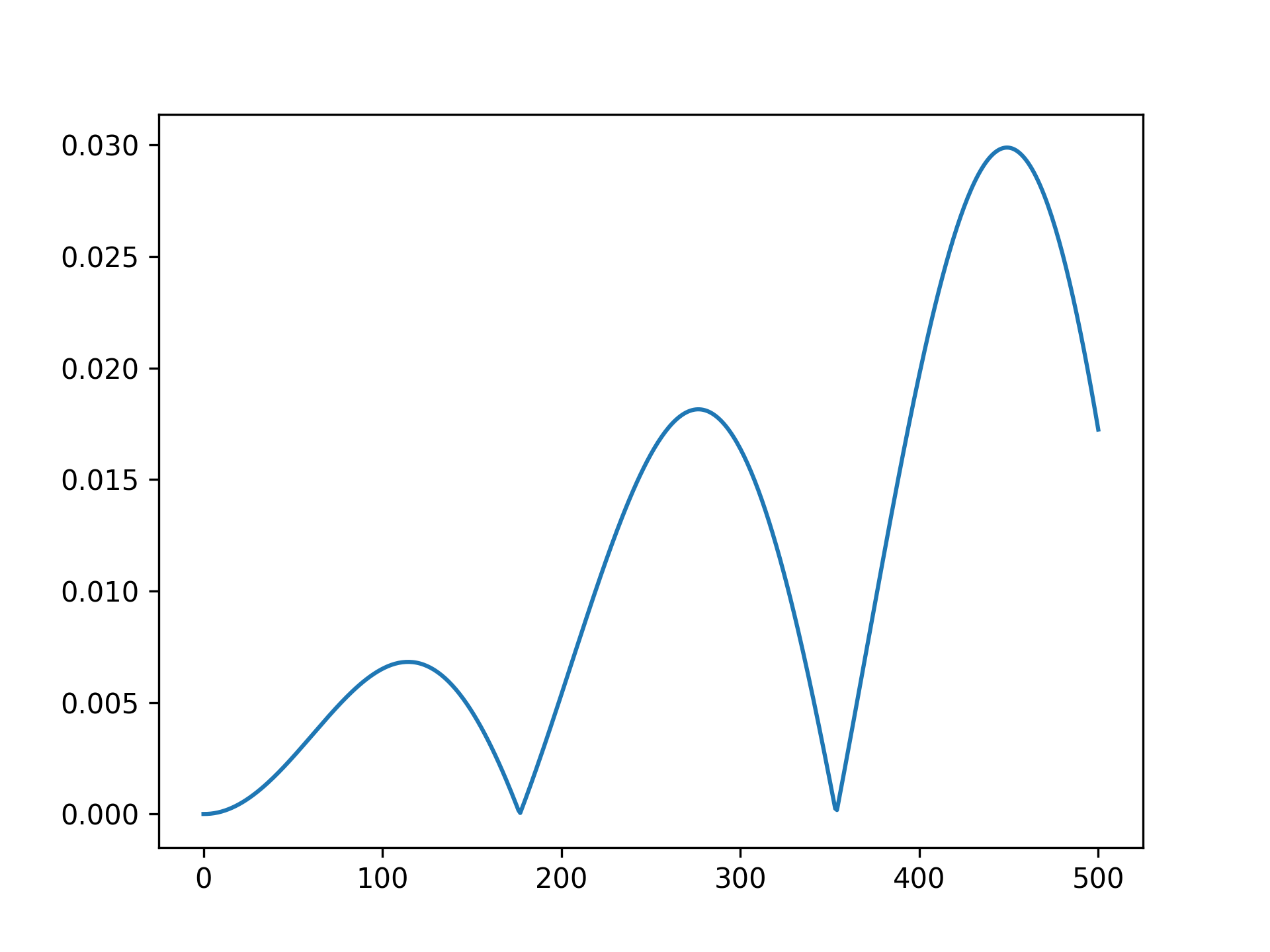
Error

最后提醒一点，为了保证模拟结果收敛，我们要保证步长比小于1：

\[\frac{\tau}{\frac{1}{2}\sqrt{h_x^2+h_y^2}}\leq 1\]

由于我们的 $r_x=r_y$ ，因此只需 $r_x\leq 1/4$ 即可。

4. Python 代码

import numpy as np
import matplotlib.pyplot as plt
import os
from PIL import Image


class WaveEquation2D:
    """
    对二维情况下的波动方程进行模拟
    使用第一类齐次边界条件
    """

    def __init__(self, Lx, Ly, Lt, N, K):
        """
        设定网格范围和划分个数
        """
        self.U = np.zeros((K+1, N+1, N+1))
        self.N = N
        self.K = K
        self.Lt = Lt
        self.Lx = Lx
        self.Ly = Ly
        self.dx = Lx/N
        self.dy = Ly/N
        self.dt = T/K
        self.rx = (self.dt/self.dx)**2
        self.ry = (self.dt/self.dy)**2
        self.X = np.arange(N+1) * self.dx
        self.Y = np.arange(N+1) * self.dy
        self.T = np.arange(K+1) * self.dt

    def set_u0(self):
        """
        定义 t=0 时刻的初值函数
        """
        Fx = np.sin(np.pi * self.X / self.Lx)
        Fy = np.sin(np.pi * self.Y / self.Ly)
        self.U[0, :, :] = np.outer(Fx, Fy)

    def set_u1(self):
        """
        通过 u0 的 Laplace 算子计算 u1
        """
        Fx = np.sin(np.pi * self.X / self.Lx)
        Fy = np.sin(np.pi * self.Y / self.Ly)
        DeltaU = -(np.pi/self.Lx)**2 * np.outer(Fx, Fy) - \
            (np.pi/self.Ly)**2 * np.outer(Fx, Fy)
        self.U[1, :, :] = self.U[0, :, :] + self.dt**2 / 2*DeltaU

    def simulation(self):
        """
        仿真模拟
        """
        ## 计算 u0
        self.set_u0()
        ## 计算 u1
        self.set_u1()
        rx = self.rx
        ry = self.ry
        ## 从 t=2 的时刻开始迭代更新
        for n in range(1, self.K):
            ##  边界处的值由边界条件确定, 我们只更新内部
            for i in range(1, self.N):
                for j in range(1, self.N):
                    self.U[n+1, i, j] = 2*(1-rx-ry)*self.U[n, i, j]
                    self.U[n+1, i, j] -= self.U[n-1, i, j]
                    self.U[n+1, i, j] += rx * \
                        (self.U[n, i+1, j]+self.U[n, i-1, j])
                    self.U[n+1, i, j] += ry * \
                        (self.U[n, i, j+1]+self.U[n, i, j-1])
            ## 更新边界条件
            self.U[n+1, [0, -1], :] = 0
            self.U[n+1, :, [0, -1]] = 0

    def animate(self):
        """
        通过动画演示, 保存为 gif 动图
        """
        if not os.path.exists("Figure"):
            os.makedirs("Figure")
        fig = plt.figure(2)
        ax = fig.add_subplot(111, projection='3d')
        X, Y = np.meshgrid(self.X, self.Y)
        imgs = []
        ## 隔 4 次计算保存一次图
        for n in range(0, self.K+1, 4):
            t = self.T[n]
            ax.plot_surface(
                X, Y, self.U[n, :, :], cmap='rainbow', linewidth=2, antialiased=False)
            ax.set_xlim3d(0, self.Lx)
            ax.set_ylim3d(0, self.Ly)
            ax.set_zlim3d(-1.5, 1.5)
            ax.set_xlabel("x")
            ax.set_ylabel("y")
            ax.set_zlabel("U")
            ax.text(1, 1, 1, "T = {:.2f}s".format(t),
                    size=plt.rcParams["axes.titlesize"],
                    ha="center", transform=ax.transAxes, )
            plt.savefig("Figure/"+str(n), dpi=300)
            print("Save figure in Figure/"+str(n)+".png")
            img = Image.open("Figure/"+str(n)+'.png')
            imgs.append(img)
            ax.cla()
        img.save('wave.gif', save_all=True, append_images=imgs, duration=0.1)

    def evaluate(self):
        """
        评估与真实函数的误差
        """
        Fx = np.sin(np.pi * self.X / self.Lx)
        Fy = np.sin(np.pi * self.Y / self.Ly)
        Fu = np.outer(Fx, Fy)
        c = np.pi*np.sqrt(1/self.Lx**2+1/self.Ly**2)
        Error = []
        for n in range(self.K+1):
            t = PDE.T[n]
            Ut = Fu*np.cos(c*t)
            err = np.linalg.norm(Ut-self.U[n, :, :])
            Error.append(err)
            ## print(err)
        self.Err = Error
        plt.figure(1)
        plt.plot(self.Err)
        plt.savefig("Error.png", dpi=300)


if __name__ == "__main__":
    Lx = 2
    Ly = 2
    T = 4
    N = 50
    K = 500
    PDE = WaveEquation2D(Lx, Ly, T, N, K)
    PDE.simulation()
    print(PDE.rx)
    print(PDE.U.shape)
    PDE.evaluate()
    PDE.animate()

5. 参考

  1. 波动方程的数值解(Mathematica) - 知乎
  2. Python数值计算—二维波动方程有限差分解 - 知乎