先通过特征提取器提取点特征，然后转化为图的形式，之后使用图特征提取器提取特征，用于更新点特征。再建图提取特征，最终通过特征向量的相似性构建相似性矩阵 $\tilde{C}$。之后将软分配的相似矩阵 $\tilde{C}$ 转化为硬分配矩阵 $C$，再通过 SVD 求解旋转矩阵和平移向量。

1. Problem Formulation

对于源点云 \(\mathbf{X}=\left\{x_i\in\mathbb{R}^3 \mid i=1,\cdots,N\right\}\) 和目标点云 \(\mathbf{Y}=\left\{y_j\in\mathbb{R}^3 \mid j=1,\cdots,M\right\}\)，点云配准的目标是找到一个旋转变换 ${\mathbf{R},\mathbf{t}}$ 来将这两个点云对齐，其中 $\mathbf{R}\in\mathbf{SO}(3)$ 为旋转矩阵, $\mathbf{t}\in\mathbb{R}^3$ 为平移向量。

而 $\mathbf{X}$ 和 $\mathbf{Y}$ 之间的对应关系用二值矩阵 \(\mathbf{C}\in \{0,1\}^{N\times M}\) 来表示：如果 $\mathbf{C}_{ij}=1$，那么表示 $x_i$ 在 $\mathbf{Y}$ 中的对应点为 $y_j$。

如果 $\mathbf{X}$ 和 $\mathbf{Y}$ 是完全等价的话，也就是每个 $x_i$ 都会在 $\mathbf{Y}$ 中有一个点 $y_j$ 与之对应。那么目标函数就可以写成

\[\boldsymbol{e}(\mathbf{C}, \mathbf{R}, \mathbf{t})=\sum_{i}^{N} \sum_{j}^{M} \mathbf{C}_{i, j}\left\|\mathbf{R} x_{i}+\mathbf{t}-y_{j}\right\|_{2}^{2}\\\]

这里 $\mathbf{C}$ 矩阵的每一行和每一列都有且只有一个位置的值为1，剩下的全为0，即

\[\sum_{j}^{M} \mathbf{C}_{i, j}=1, \forall i,\ \sum_{i}^{N} \mathbf{C}_{i, j}=1, \forall j,\ \mathbf{C}_{i, j} \in\{0, 1\}^{N \times M}, \forall i, j\\\]

但是在实际情况中，有可能会出现 $x_i$ 在 $Y$ 中没有对应点的情况，这时等式约束就从 \(\sum_{j}^{M} \mathbf{C}_{i, j}=1\) 变成了不等式约束 \(\sum_{j}^{M} \mathbf{C}_{i, j}\leq 1\)。作者对此的应对方法是添加一个松弛变量 $\mathbf{C}_{i,M+1}$，使得约束条件重新变成等式约束：

\[\sum_{j}^{M} \mathbf{C}_{i, j} \leq 1, \forall i \rightarrow \sum_{j}^{M+1} \mathbf{C}_{i, j}=1, \forall i \leq N\\\]

这里的 $\mathbf{C}$ 为一个 $(N+1)\times(M+1)$ 的矩阵。

在确定了对应关系之后，就可以使用 SVD 方法求解了。

2. RGM 网络

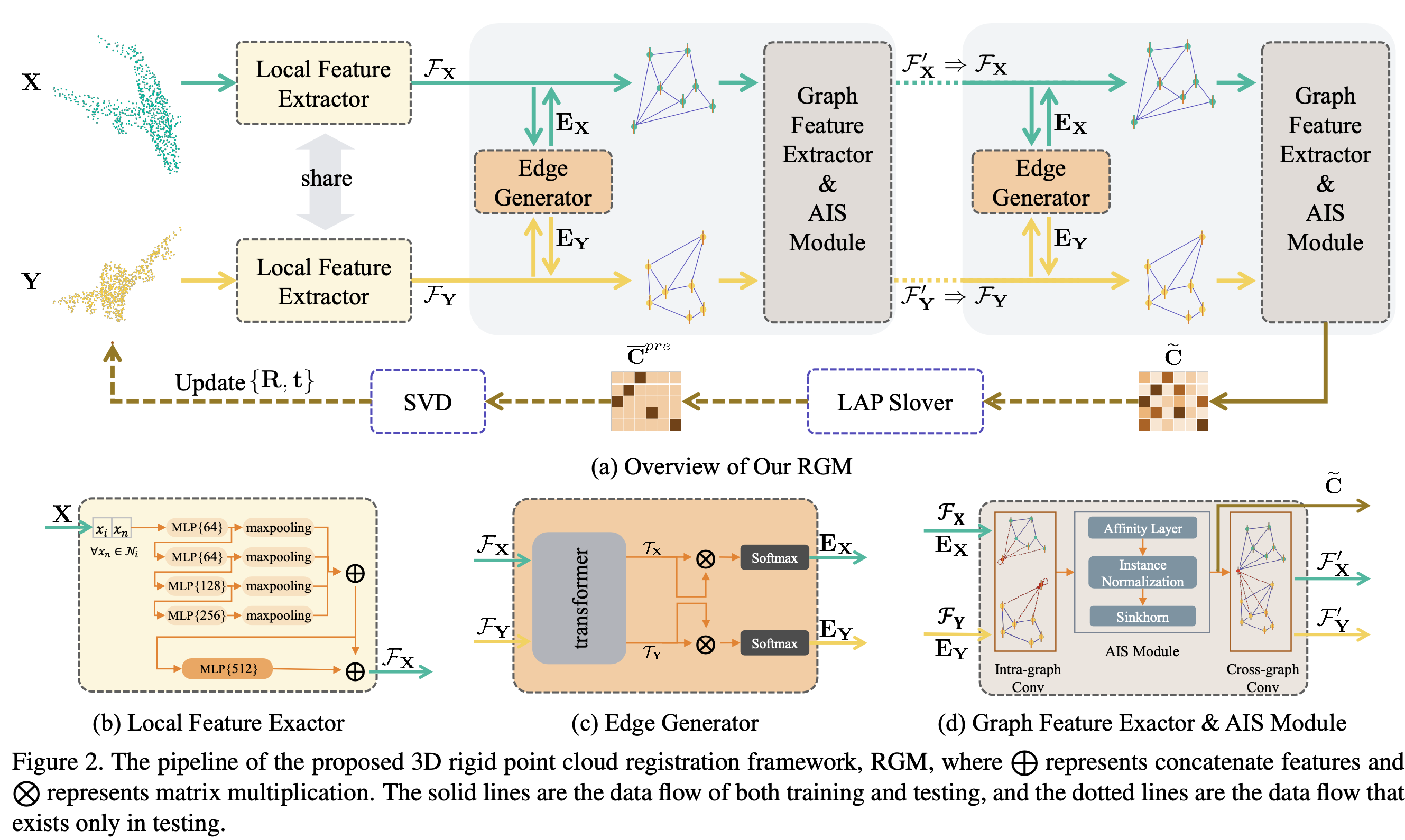
图2就是整个 RGM 网络的 pipeline，主要分成4个部分：

  1. Local Feature Extractor
  2. Edge Generator
  3. Graph Feature Extractor and AIS Module
  4. LAP Slover and SVD

2.1. Local Feature Extractor

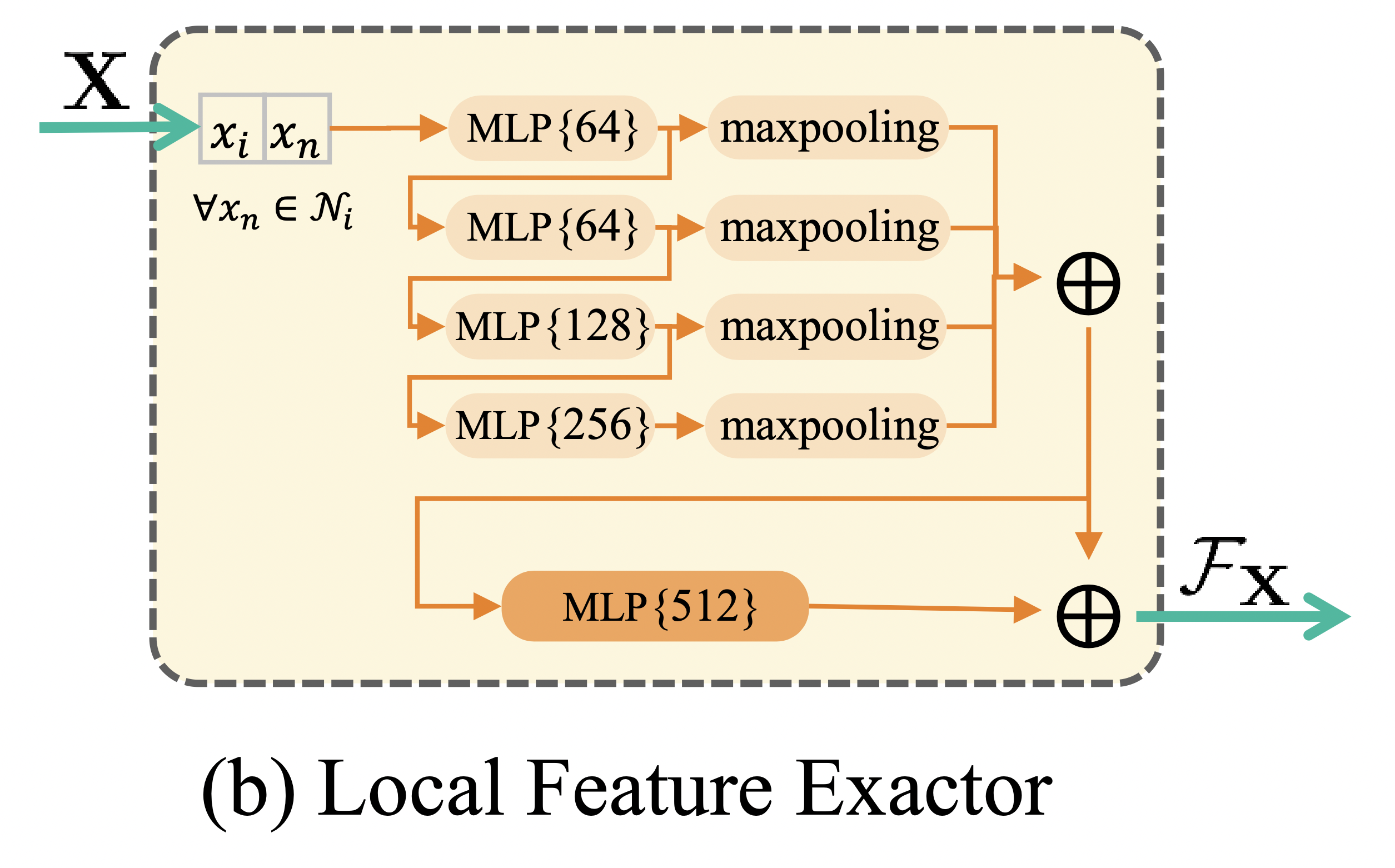
首先是使用局部特征提取器来提取点云的局部特征，对于每一个点 $x_i$，其 local feature descriptor 表示为：

\[\mathcal{P}_{x_{i}}=\left\{\left(x_{i}, x_{n}\right) \mid \forall x_{n} \in \mathcal{K}_{i}\right\}\\\]

$\mathcal{K}_i$ 表示 $x_i$ 的 $K$ 个最近邻。

可以看到，\(\mathcal{P}_{x_i}\) 是一个 $\mathbb{R}^{K\times6}$ 的矩阵，通过 $f_\theta$ 将其映射到一个 $V$ 维向量 \(\mathcal{F}_{x_{i}}\)，即

\[\mathcal{F}_{x_{i}}=f_{\theta}\left(\mathcal{P}_{x_{i}}\right).\\\]

图(b)为特征提取器的网络结构，将不同MLP层的向量拼接起来，这样可以提取到多尺度的特征。最终对于每个点 $x_i$，都生成了一个512维的特征向量 \(\mathcal{F}_{x_{i}}\)。

注意这里的 $\mathbf{X}$ 和 $\mathbf{Y}$ 都是共用相同的网络参数，这样的话点云越相似，那么生成的特征向量也会更相似。

然而只使用局部特征向量的话，很难准确预测点与点之间的对应关系，因为只包含了局部信息，缺乏全局的结构信息。因此作者提出通过点云建图，然后用深度图匹配(deep graph matching)来建立对应关系。

2.2. Edge Generator Based on Transformer

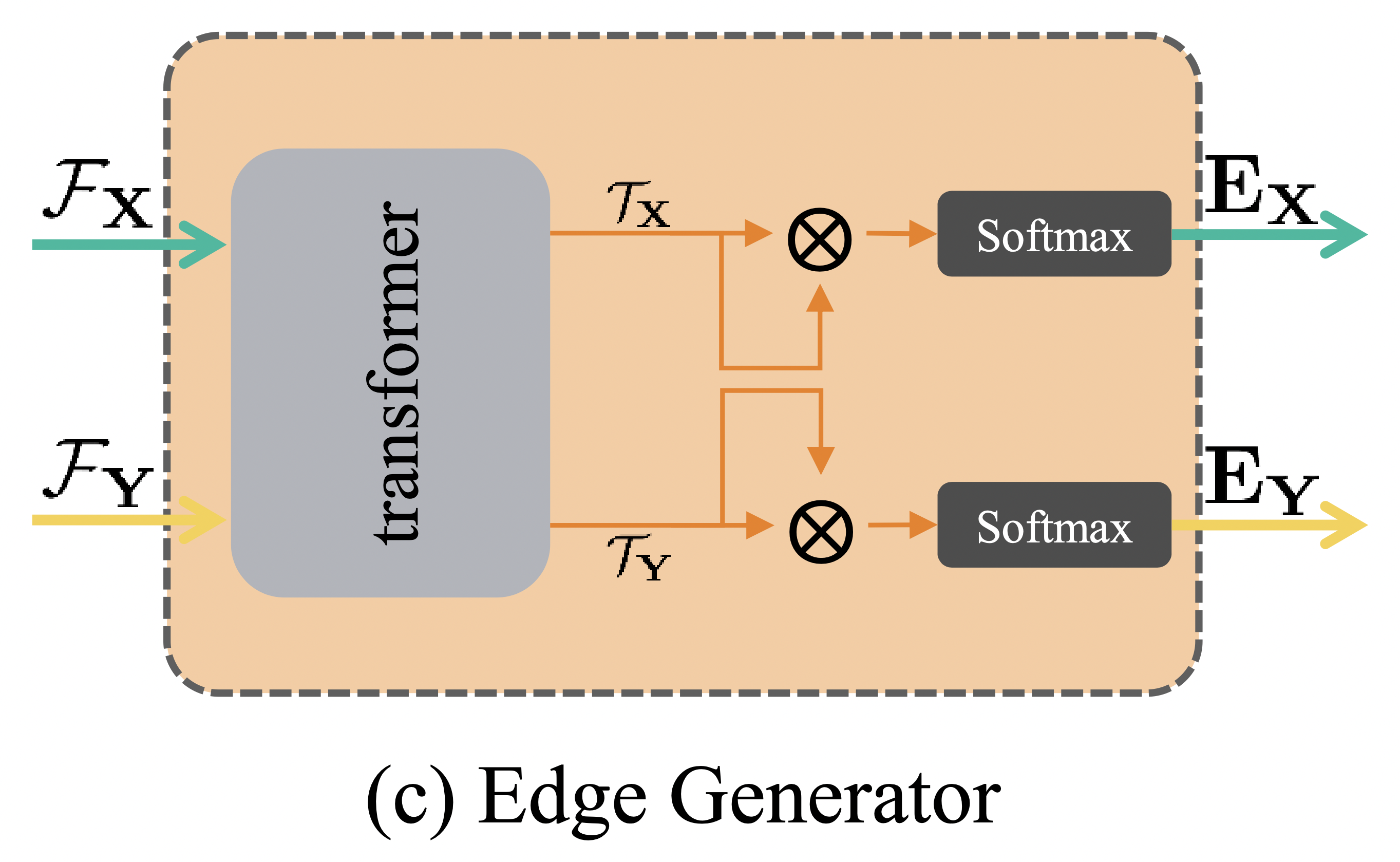
将从 $\mathbf{X}$ 和 $\mathbf{Y}$ 生成的图记为 source graph \(\mathcal{G}_s=\left\{\mathbf{X},\mathbf{E}_\mathbf{X}\right\}\) 和 target graph \(\mathcal{G}_t=\left\{\mathbf{Y},\mathbf{E}_\mathbf{Y}\right\}\)。 这里的 $\mathbf{E}$ 为邻接矩阵。

从点云建图的方法有 full connection, nearest neighbor connection 和 Delaunay triangulation，但是这些方法不能有效地聚合图的特征。于是作者使用了 NLP 中很火的 transformer，来学习节点之间的软连接关系。

图(c)为边生成器的网络结构，transformer由几个堆叠的编码器和解码器组成，编码器使用了 self-attention 和 shared MLP，而解码器是基于 co-attention 机制。

Transformer 将节点特征 \(\mathcal{F}_\mathbf{X}\) 和 \(\mathcal{F}_\mathbf{Y}\) 作为输入，然后将它们编码成嵌入特征(embedding feature) \(\mathcal{T}_\mathbf{X}\) 和 \(\mathcal{T}_\mathbf{Y}\):

\[\mathcal{T}_{\mathbf{X}}, \mathcal{T}_{\mathbf{Y}}=f_{\text {transformer}}(\mathcal{F}_{\mathbf{X}}, \mathcal{F}_{\mathbf{Y}})\\\]

边的软邻接矩阵通过特征向量的内积，再接一个 softmax 归一化来表示：

\[\mathbf{E}_{\mathbf{X}}=\operatorname{softmax}(\langle\left(\mathcal{T}_{\mathbf{X}}\right)^{T}, \mathcal{T}_{\mathbf{X}}\rangle)\\\] \[\mathbf{E}_{\mathbf{Y}}=\operatorname{softmax}(\langle\left(\mathcal{T}_{\mathbf{Y}}\right)^{T}, \mathcal{T}_{\mathbf{Y}}\rangle)\\\]

2.3. Graph Feature Extractor

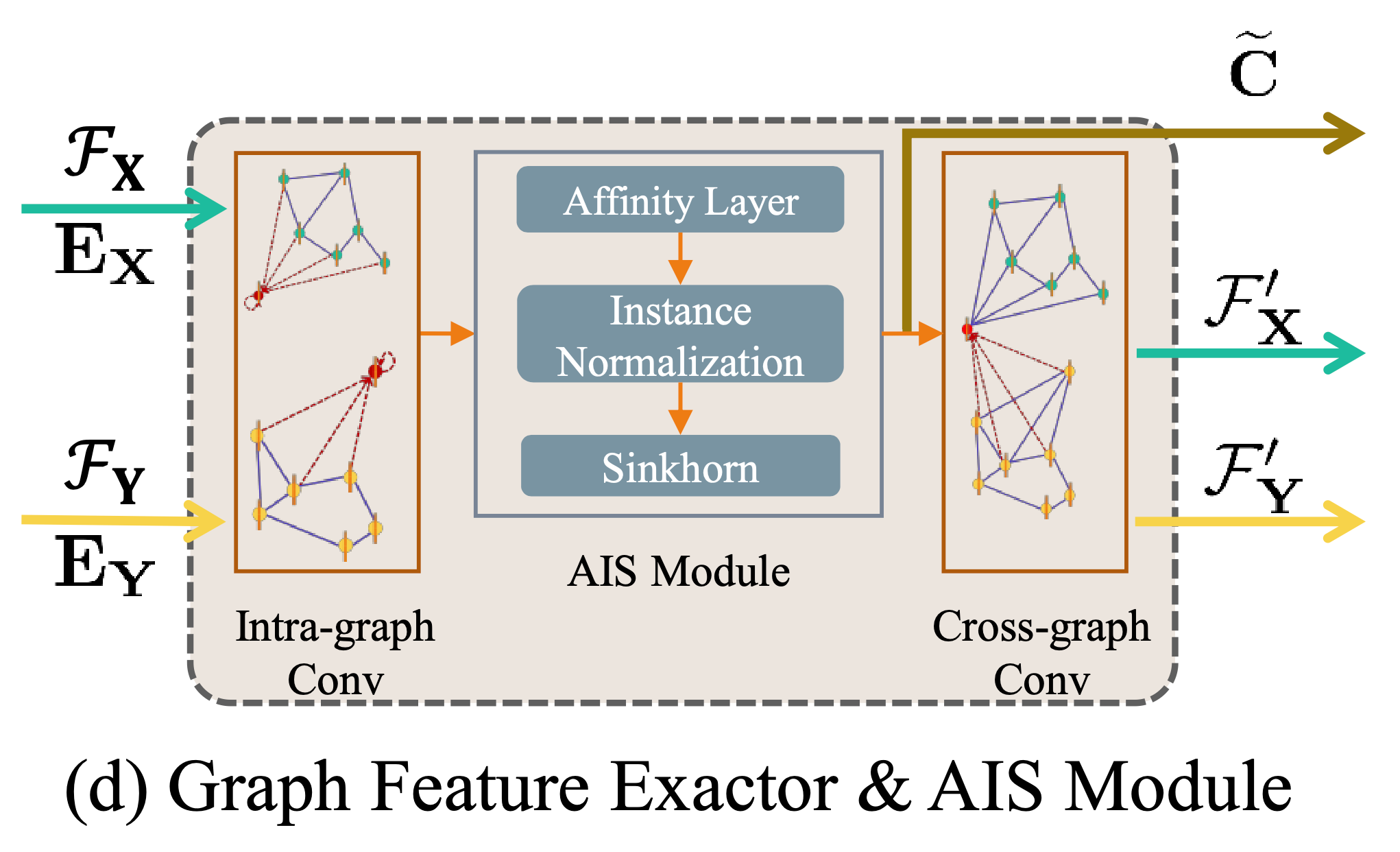
在得到了图结构之后，就可以用图特征提取器来提取特征了，首先通过图内卷积(intra-graph convolution) 计算图 \(\mathcal{G}_s=\left\{\mathbf{X},\mathbf{E}_\mathbf{X}\right\}\) 的结构特征 $\mathcal{F}_{x_i}^{corr}$：

\[\mathcal{F}_{x_{i}}^{corr}=\sum_{j=1}^{N}\breve{\mathbf{E}}_{i, j} * f_{adj}(\mathcal{F}_{x_{j}})+f_{self}(\mathcal{F}_{x_{i}})\\\]

文中表示 $\breve{\mathbf{E}}$ 是从 ${\mathbf{E}}$ 归一化得来的，但我很疑惑，${\mathbf{E}}$ 本身不就已经通过 softmax 归一化了吗？

这个结构其实就是普通的GNN模型，如果从消息传播的角度来说，$f_{adj}$ 表示从邻居节点汇合信息， $f_{self}$ 表示自身信息。

2.4. AIS Module

在提取完图特征之后，用 AIS 模块来计算软对应矩阵。AIS 模块由 affinity layer, instance normalization 和 Sinkhorn 三部分组成。

2.4.1. Affinity Layer

Affinity Layer 用于计算两个图之间的相似性。

两个图之间的相似度矩阵 $\mathbf{A}$ 通过结构特征 $\mathcal{F}^{corr}$ 来计算：

\[\mathbf{A}_{i, j}=(\mathcal{F}_{x_{i}}^{corr})^{T} \mathbf{W}(\mathcal{F}_{y_{j}}^{corr})\\\]

这里 $\mathbf{W}$ 是神经网络中的可学习参数。

2.4.2. Instance Normalization

在计算出 $\mathbf{A}$ 之后，还有一个问题，就是此时矩阵中的值可能是负的，因此还需要进行归一化。通常的做法是按行或列 softmax 归一化，但可能带来的问题是会改变行或列之间的大小关系，例如图3中，本来虚线框内最大的元素是(5,2)，但在按列归一化之后，最大的元素变成了(2,1)。

为了避免这种情况，作者使用了 Instance Normalization，可以看这篇文章 模型优化之Instance Normalization - 知乎 简单了解一下，下面这张图就是各种归一化方法的差异。

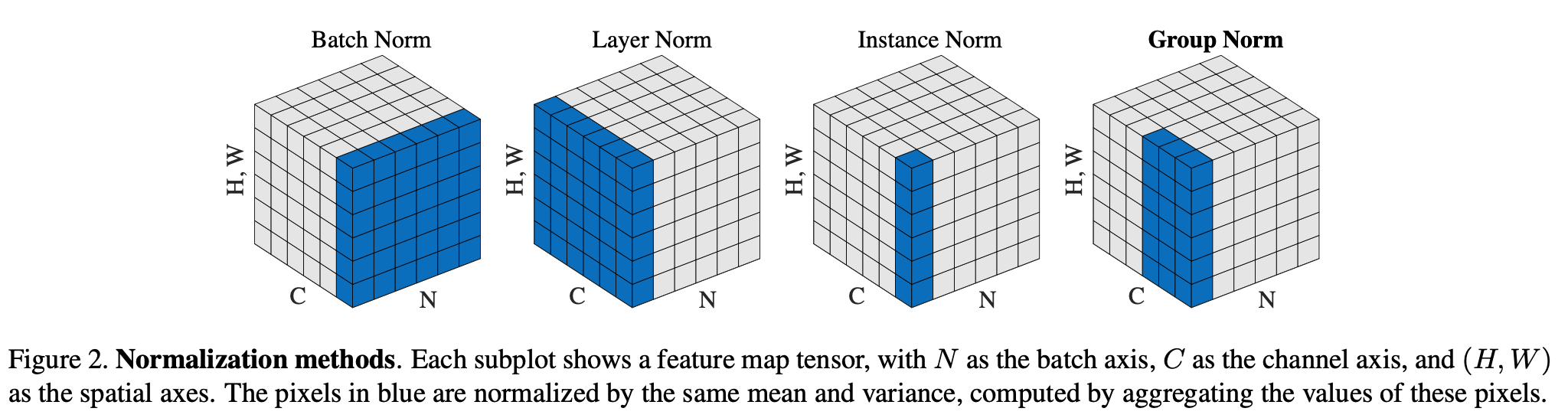
2.4.3. Sinkhorn Layer

关于这个 Sinkhorn Layer，论文中只提了一句：

Using Sinkhorn to compute the soft correspondence matrix $\widetilde{\mathbf{C}}$.

然后就跳过去了，由于这篇论文参考的是 ICCV2019 的《Learning Combinatorial Embedding Networks for Deep Graph Matching》，所以我们找到该论文中对于 Sinkhorn Layer 的描述。

说白了，就是先行归一化，再列归一化，反复迭代，最后得到软对应矩阵 $\widetilde{\mathbf{C}}$。

说实话这个 Instance Normalization 和 Sinkhorn Layer 感觉非常牵强，没看出有啥意义。

2.4.4. Cross-graph conv

在得到软对应矩阵 $\widetilde{\mathbf{C}}$ 之后，作者用图间卷积(cross-graph conv)来增强特征的图间相关性：

\[\mathcal{F}_{x_{i}}^{\prime}=f_{\text {cross}}(\mathcal{F}_{x_{i}}^{\text {corr}}, \sum_{j=1}^{\mathrm{M}} \widetilde{\mathbf{C}}_{i, j} * \mathcal{F}_{y_{j}}^{\text {corr}})\\\]

如果 $x_i$ 和 $y_j$ 越相似，那么 \(\mathcal{F}_{x_{i}}^{\text {corr}}\) 和 \(\sum_{j=1}^{\mathrm{M}} \widetilde{\mathbf{C}}_{i, j} * \mathcal{F}_{y_{j}}^{\text {corr}}\) 也会越相似，最终得到新的节点特征 \(\mathcal{F}_{x_{i}}^{\prime}\)。

2.5. LAP Slover and SVD

由于 $\widetilde{\mathbf{C}}$ 为软对应矩阵，因此作者使用基于匈牙利算法的 LAP 求解器将其转化为一个 0-1 矩阵 ${\overline{\mathbf{C}}}^{pre}$， 然后使用 SVD 求解。

其实感觉这个也没必要，转化为硬分配矩阵，增加了步骤不说，而且还降低了鲁棒性。

2.6. Loss

作者考虑到 SVD 步骤是不可微的，所以并不是用配准结果作为衡量，而是用 $\widetilde{\mathbf{C}}$ 与 ground-truth 对应矩阵 $\overline{\mathbf{C}}^{gt}$ 的交叉熵作为 loss 函数：

\[\text{loss}=-\sum_{i}^{N}\sum_{j}^{M}(\overline{\mathbf{C}}_{i, j}^{g t} \log \widetilde{\mathbf{C}}_{i, j}+(1-\overline{\mathbf{C}}_{i, j}^{g t})\log(1-\widetilde{\mathbf{C}}_{i, j}))\\\]

其实 SVD 过程是可微的，参考 Deep Closest Point，当然这样也不错。

3. 实验

在 ModelNet40 数据集上进行测试，对于每个模型，从网格中采样出 2048 个点并缩放到单位球上。作者随机取 1024 个点作为源点云 $\mathbf{X}$，然后对 $\mathbf{X}$ 做一个旋转变换得到目标点云 $\mathbf{Y}$， 旋转角范围为 $[0,45]^{\circ}$ ，位移范围为 $\left[-0.5,\ 0.5\right]$。

评估标准有6个：

  • Mean isotropic errors (MIE) of $\mathbf{R}$ and $\mathbf{t}$ proposed in RPM-Net
  • Mean absolute errors (MAE) of $\mathbf{R}$ and $\mathbf{t}$ used in DCP
  • Clip chamfer distance (CCD)
\[\operatorname{CCD}(\widehat{\mathbf{X}}, \mathbf{Y})=\sum\limits_{\hat{x}_{i} \in \mathbf{X}}\min(\min\limits_{y_{j} \in \mathbf{Y}}(\left\|\hat{x}_{i}-y_{j}\right\|_{2}^{2}), d) +\sum\limits_{y_{j} \in \mathbf{Y}}\min(\min\limits_{\hat{x}_{i} \in \mathbf{X}}(\left\|\hat{x}_{i}-y_{j}\right\|_{2}^{2}), d)\\\]

这里的 $\hat{\mathbf{X}}$ 是旋转后的源点云。

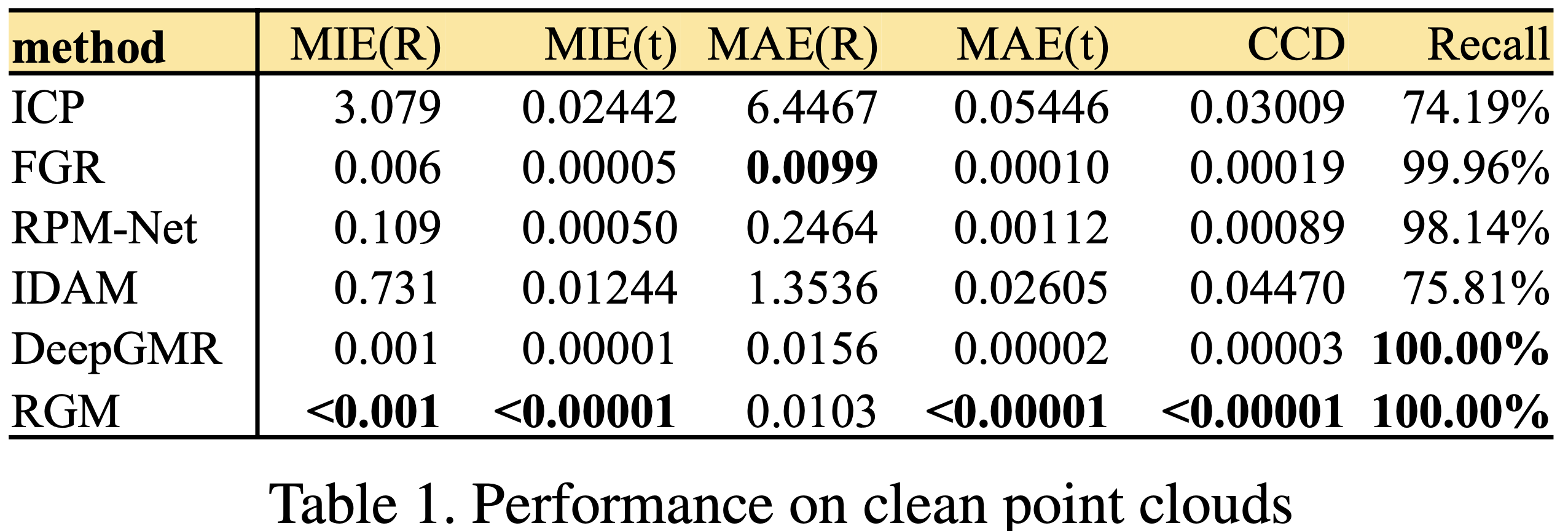
整体的实验结果如下：

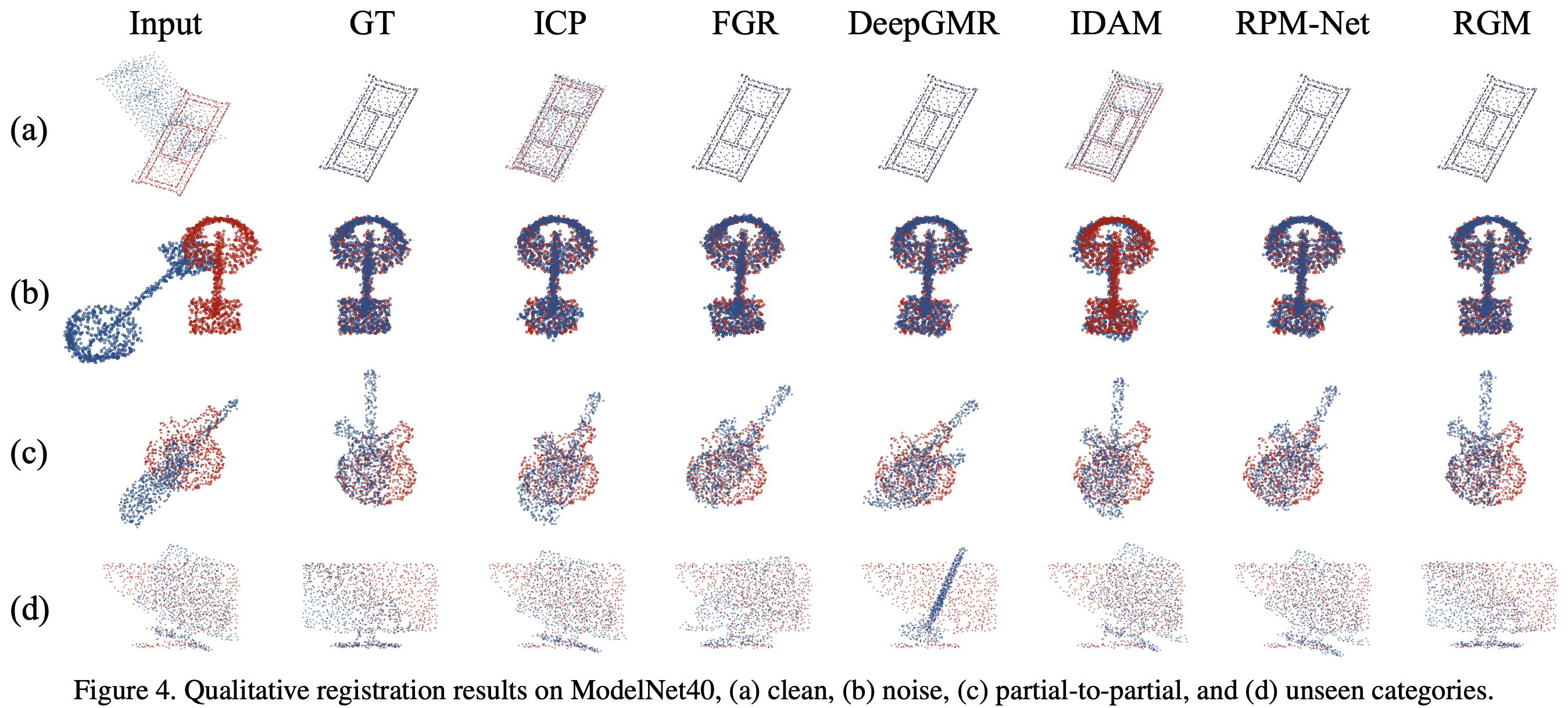
3.1. Clean Point Cloud

3.2. Gaussian Noise

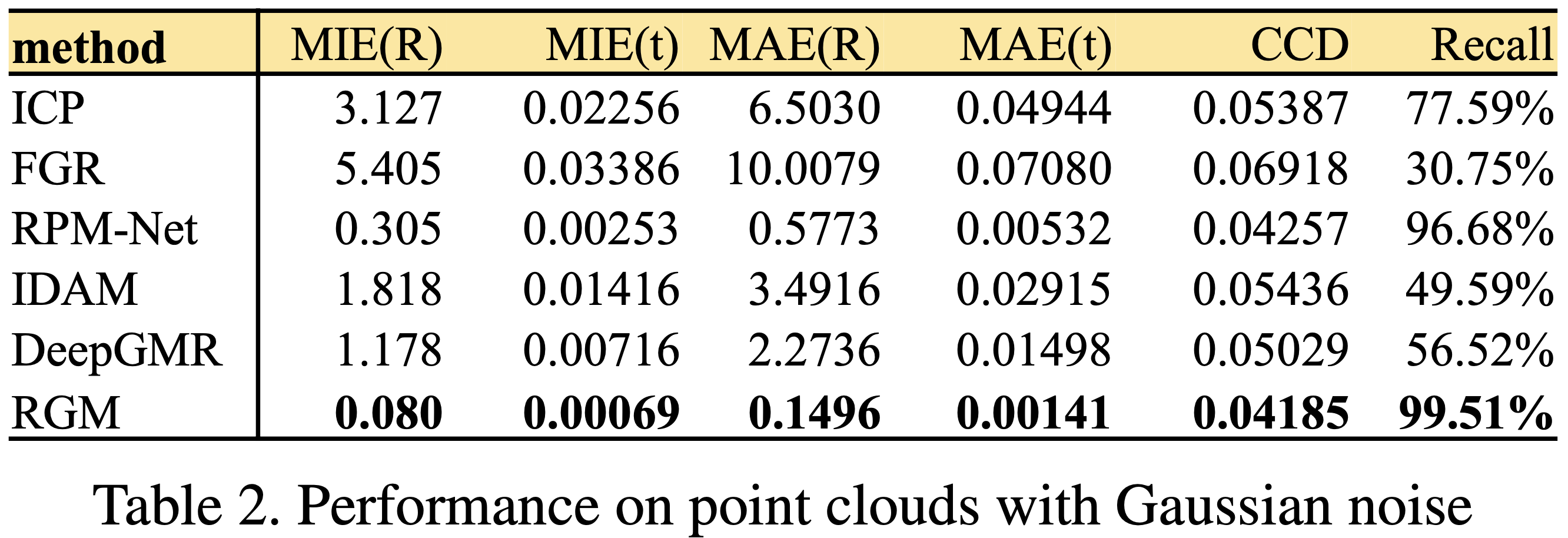
添加 $\mathcal{N}\left(0,\ 0.01\right)$ 的高斯噪声和随机位移 $\left[-0.05,\ 0.05\right]$。

3.3. Partial-to-Partial

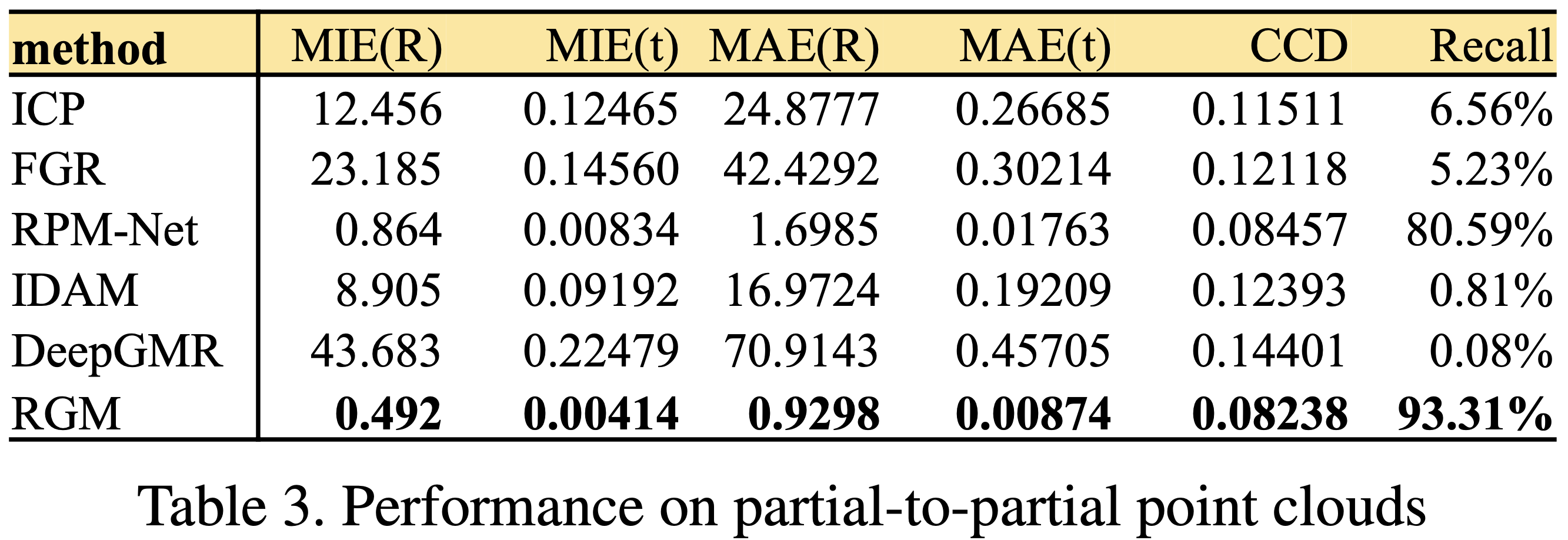
参考 RPM- Net，使用随机平面切掉 30% 的点。

3.4. Unseen Categories

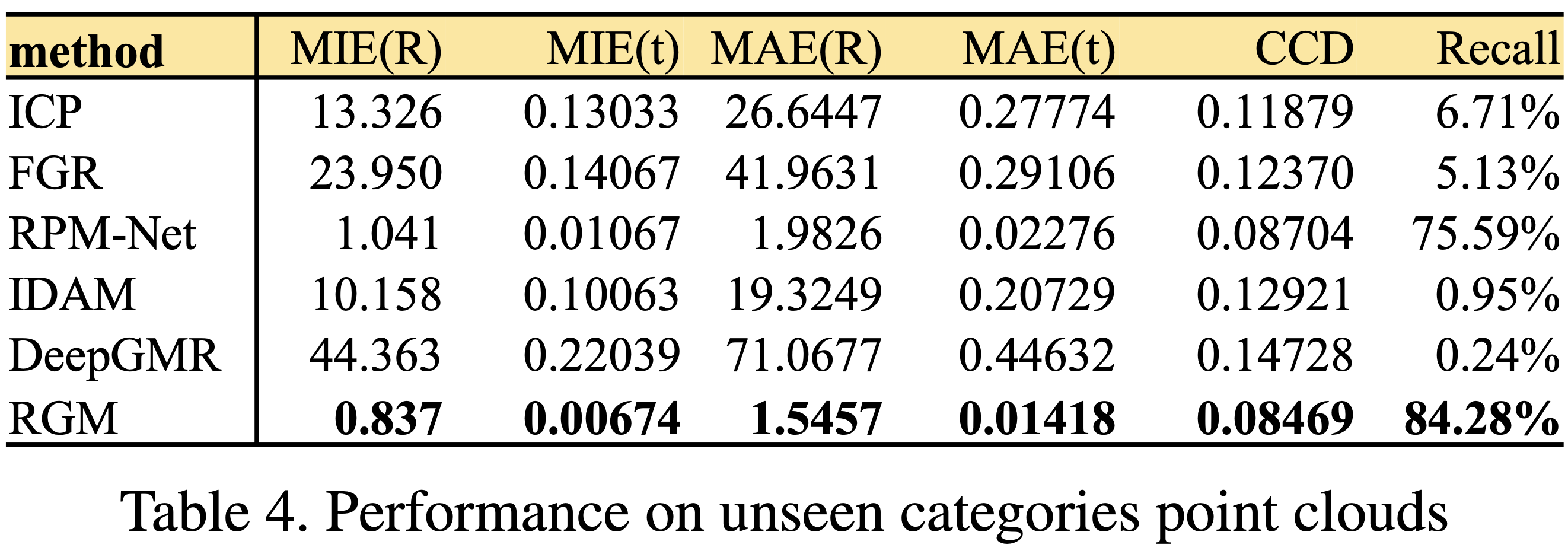
为了测试泛化能力，在20个未训练种类的物体上进行测试。

3.5. Ablation Studies

为了测试 AIS 模块到底有没有用，作者设计了消融实验。

变体1：用 $e^{-\left(\mathbf{D}_{i,j}\ -\ 0.5\right)}$ 代替AIS模块来计算特征间的相似性，然后用 Sinkhorn 计算软对应矩阵 $\widetilde{\mathbf{C}}$。这里 $\mathbf{D}$ 表示节点特征间的 L2 距离。

变体2：将基于 transformer 的边生成器，替换为全连接边。

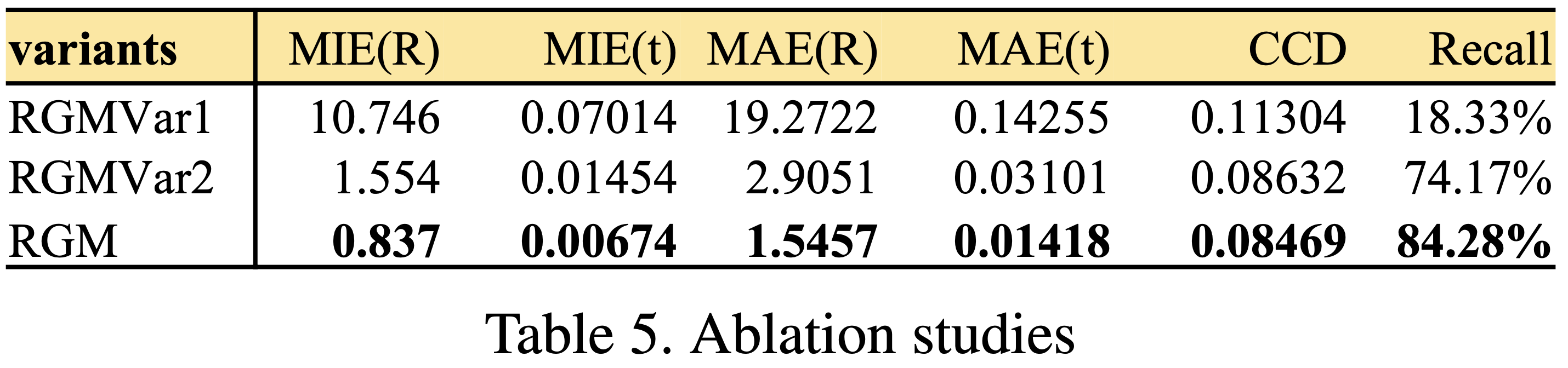
那么我收回之前的话，AIS 模块还是很有用的。。。

4. 总结

整体来看，模型的设计还是不错的。以下为一些个人观点：

  1. 使用 transformer 来生成边，这个方法还是缺乏实际意义。虽然进行了消融实验，但只能证明全连接的建图方法不适合该网络。 如果能将生成的图可视化出来，让我们观察到 transformer 生成的图到底长什么样，这样会更有说服力。
  2. SVD 如果用软对应矩阵会是什么样的结果呢？如果准确率降低了问题出在哪?
  3. 在实际生活的场景中，配准效果如何？网络的推理速度如何？
  4. 对于配准失败的例子，瓶颈是在哪一步呢？