PAC 学习框架
本文参考《Foundation of machine learning》,总结了 PAC 学习框架。
1. PAC 学习模型
1.1. 基础定义
Probably Approximately Correct (PAC),即概率近似正确。PAC 学习可以分为两部分:
- 近似正确( Approximately Correct ):一个假设 $h\in \mathcal{H}$ 是“近似正确”的,是指其在泛化错误 $R(h)$ 小于一个界限 $\epsilon$,$\epsilon$ 一般为趋于0的一个数,如果 $R(h)$ 比较大,说明模型不能用来做正确的“预测”.
- 可能( Probably ):一个学习算法 $\mathcal{A}$ 有“可能”以 $1-\delta$ 的概率学习到这样一个“近似正确”的假设.
一个 PAC 可学习( PAC-Learnable )的算法是指该学习算法能够在多项式时间内从合理数量的训 练数据中学习到一个近似正确的假设 $h$.

$h_S$ 表示在样本 $S$ 上学习到的假设 ,$R(h_S)$ 表示 $h_S$ 的泛化误差。
该公式表明:对于任意小的 $\epsilon,\delta$, 只要样本个数 $m$ 足够大(能被关于 $1/\epsilon,1/\delta,size(c)$ 的多项式表示),就能以 $1-\delta$ 的概率使 $R(h_S)\leq \epsilon$ 成立.
这样的概念类 $\mathcal{C}$ 称为PAC可学的(PAC-learnable)
1.2. 沿轴矩形的学习(axis-aligned rectangles)
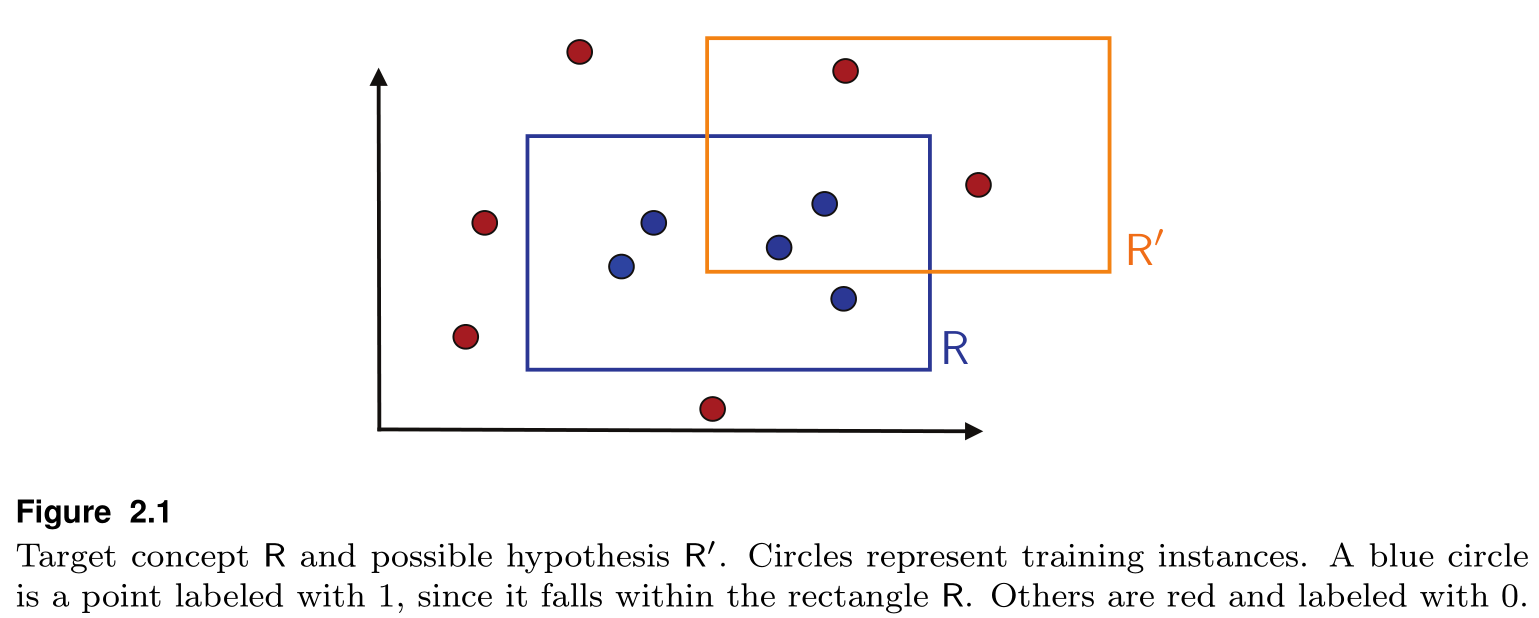
$R$ 是我们要学习的矩形框,矩形框内的样本为正例,框外的样本为负例,$R’$ 是可能的一个假设.
我们可以证明这种矩形框是PAC可学的——我们设定一个简单的算法:取包裹所有正例样本的最小矩形框,就像这样:
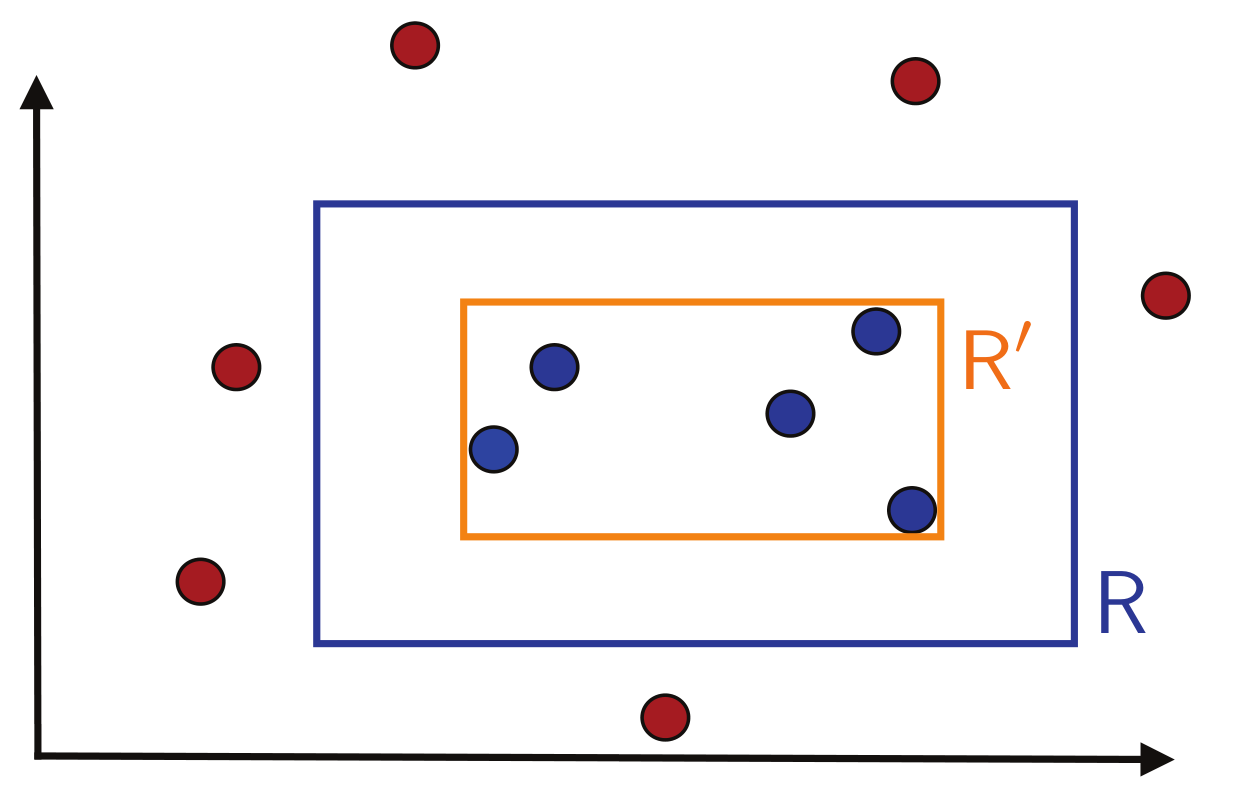
首先,我们先假设样本点由随机分布 $\mathcal{D}$ 产生,用 $\mathbb{P}[R]$ 表示 $R$ 区域的概率质量,即一个样本点落在 $R$ 中的概率.
我们先定义假设框 $R_S$ 的泛化误差 $\mathcal{R}(R_S)$:样本点落在 $R-R_S$ 区域的期望.
之后我们做一个假设 :
\[\mathbb{P}\left[ R \right] >\epsilon\]否则, $\mathcal{R}(R_S)<\epsilon$ 显然恒成立.
然后,我们在矩形的四边构建 4 个小矩形 $r_1,r_2,r_3,r_4$,使得 $\mathbb{P}[r_i]=1/4$.
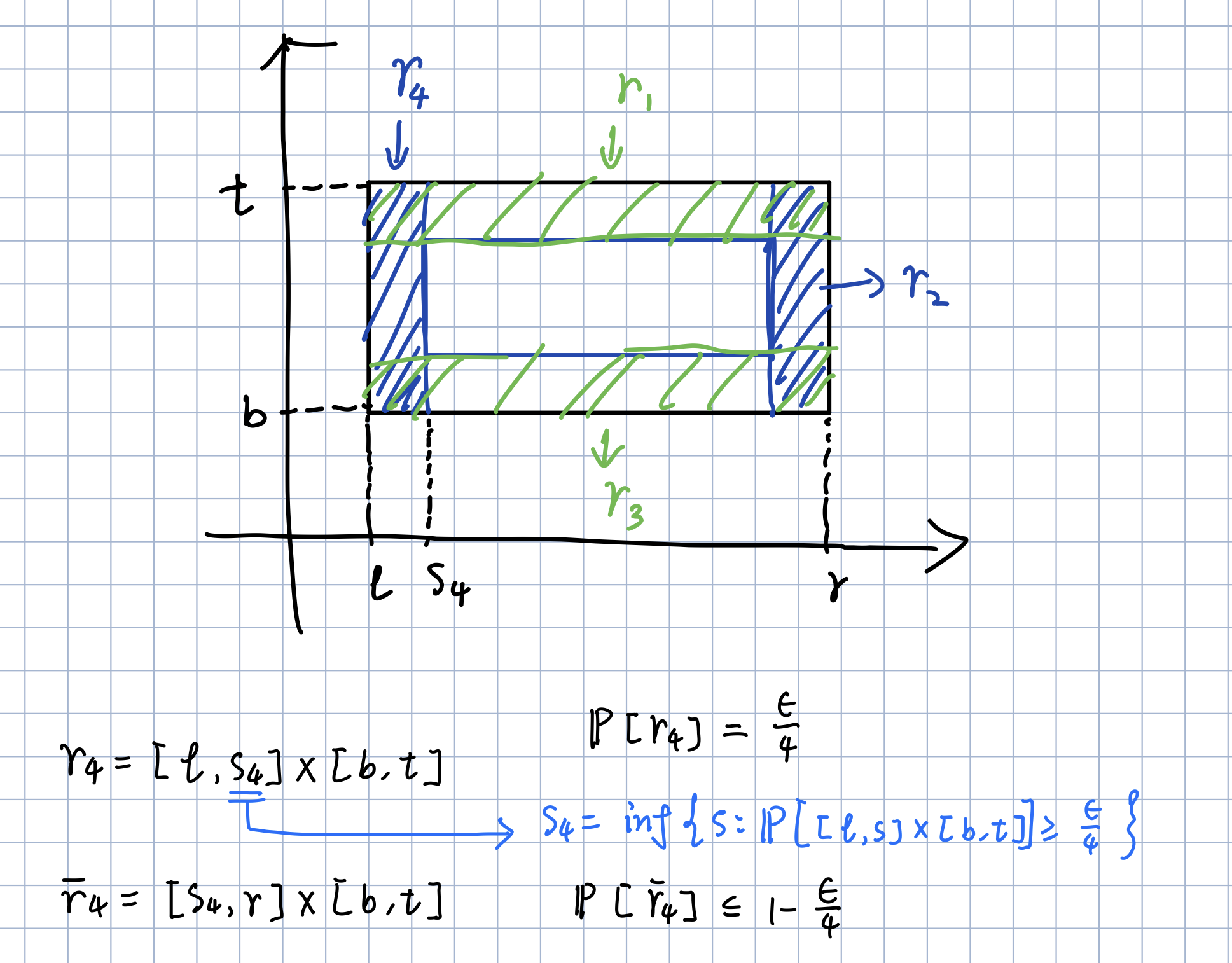
我们记周围这一圈阴影部分为 $r=\bigcup_{i=1}^4{r_i}$,显然有:
\[\mathbb{P}\left[ r \right] =\mathbb{P}\left[ \bigcup_{i=1}^4{r_i} \right] \le \sum_{i=1}^4{\mathbb{P}\left[ r_i \right]}\le \epsilon\]如果我们的假设框 $R_S$ 的四条边都在阴影部分 $r$ 中,即 $R-r\subset R_S$ ,那么有:
\[\mathcal{R}(R_S)=\mathbb{P}\left[ r-R_S \right] <\mathbb{P}\left[ r \right] \le \epsilon\]那么我们考虑其逆否命题:
若 $\mathcal{R}[R_S]>\epsilon $ ,可推出 $R-r \nsubseteq R_S$,也就是说 $R_S$ 至少与 $r_i$ 中的某一个相交为空集,即: \(\bigcup_{i=1}^4{\left\{ R_S\cap r_i=\emptyset \right\}}\)
$A\Rightarrow B$ 说明 $A\subseteq B$,即 $P\left[ A \right] \le P\left[ B \right] $.
于是上述命题可转化为公式形式:
\[\begin{aligned} \underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right] &\leq \underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \bigcup_{i=1}^4{\left\{ R_S\cap r_i=\emptyset \right\}} \right]\\ &\leq \sum_{i=1}^4{\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \left\{ R_S\cap r_i=\emptyset \right\} \right]}\\ &\leq 4\left( 1-\frac{\epsilon}{4} \right) ^m\\ &\leq 4\exp \left( -m\epsilon /4 \right) \end{aligned}\]其中第3行到第4行的转化是重点:我们的假设框 $R_S$ 是由样本 $S$ 生成的,如果假设框与 $r_i$ 不相交,那么必然没有样本点落在 $r_i$ 内,对于 $m$ 个样本点都没落进的概率为 $\left( 1-\frac{\epsilon}{4} \right) ^m$.
如果我们要使 $\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right] <\delta $ 恒成立,那么需使:
\[4\exp \left( -m\epsilon /4 \right) <\delta\]解得:
\[m>\frac{4}{\epsilon}\ln \frac{4}{\delta}\]最终得出结论:
当 $m>\frac{4}{\epsilon}\ln \frac{4}{\delta}$,时,有 $\underset{S\sim \mathcal{D}^m}{\mathbb{P}}\left[ \mathcal{R}[R_S]>\epsilon \right]<\delta$ 成立.
1.3. 泛化界
除此之外,PAC可学性的另一种等价描述可以由泛化界(generalization bound)表示:
在 $1-\delta$ 的概率下,泛化误差有关于 $m,\delta$ 表示的上界:
\[\mathcal{R}[R_S]\leq \frac{4}{m}\ln\frac{4}{\delta}\]
2. 有限假设集上的学习保证——一致情况
2.1. 一致(consistent)
有限假说集的学习问题划分为两大类:
- 一致
- 不一致
对于有限假设集 $\mathcal{H}$ ,我们要学习的目标概念 $c$ 可能在 $\mathcal{H}$ 中,也可能不在.
如果 $c\in\mathcal{H}$ ,那么称为一致情况(consistent case).
对于一致性的情况,我们能找到假设 $h_S\in \mathcal{H}$ 使得其在 $S$ 上的经验误差为0,即 $\widehat{R}(h_S)=0$ .
上面那个矩形学习的例子明显是一致的:学到的假设框 $h_S$ 在样本 $S$ 上没有误差.
2.2. 学习界(Learning bound)

该定理给出了一般性的结论:对于有限假设集 $\mathcal{H}$ ,如果学习算法 $\mathcal{A}$ 每次学到的假设 $h_S$ 都是一致的——经验误差为0,那么 $\mathcal{A}$ 为 PAC可学算法,并且给出了样本复杂度与泛化界.
可以看到,随着样本数 $m$ 的增大,泛化误差减少的速率为 $O(1/m)$.
证明:
定义
\[\mathcal{H}_{\epsilon}=\left\{ h\in \mathcal{H}:R\left( h \right) >\epsilon \right\}\]对于单个样本 $x$,有:
\[\mathbb{P}\left[ h\left( x \right) =c\left( x \right) \mid h\in \mathcal{H}_{\epsilon} \right] \le 1-\epsilon\]那么对于样本 $S\sim \mathcal{D}^m$,有:
\[\mathbb{P}\left[ \widehat{R}_S\left( h \right) =0\mid h\in \mathcal{H}_{\epsilon} \right] \le \left( 1-\epsilon \right) ^m\]那么存在 $h\in \mathcal{H}_{\epsilon} $ 使得 $ \widehat{R}_S\left( h \right) =0$ 的概率为:
\[\begin{aligned} \mathbb{P}\left[\exists h \in \mathcal{H}_{\epsilon}: \widehat{R}_{S}(h)=0\right] &=\mathbb{P}\left[\widehat{R}_{S}\left(h_{1}\right)=0 \vee \cdots \vee \widehat{R}_{S}\left(h_{\left|\mathcal{H}_{\epsilon}\right|}\right)=0\right] \\ & \leq \sum_{h \in \mathcal{H}_{\epsilon}} \mathbb{P}\left[\widehat{R}_{S}(h)=0\right] \\ & \leq \sum_{h \in \mathcal{H}_{\epsilon}}(1-\epsilon)^{m} \leq|\mathcal{H}|(1-\epsilon)^{m} \leq|\mathcal{H}| e^{-m \epsilon} \end{aligned}\]由于:学到的一致假设 \(h_S \in\mathcal{H}_{\epsilon}\) 的概率 \(\leq\) 存在一致假设 \(h\in \mathcal{H}_{\epsilon}\) 的概率
\[\mathbb{P}\left[ h_S\in \mathcal{H}_{\epsilon} \right] \le \mathbb{P}\left[ \exists h\in \mathcal{H}_{\epsilon}:\widehat{R}_S(h)=0 \right] \le |\mathcal{H}|e^{-m\epsilon}\]要使:
\[\mathbb{P}\left[ h_S\in \mathcal{H}_{\epsilon} \right]\leq \delta\]需使:
\[|\mathcal{H}|e^{-m\epsilon}\le \delta\]解得:
\[m\ge \frac{1}{\epsilon}\left( \ln |\mathcal{H}|+\ln \frac{1}{\delta} \right)\]
2.3. 布尔变量的组合

假如我们需要学习的概念类 $\mathcal{C}_n$ 为 $n$ 个布尔变量(Boolean literals)的组合,例如当 $n=4$ 时,目标概念可以是 $x_1\land \bar{x}_2\land x_4$,那么对于这个目标概念而言,$(1,0,0,1)$ 是一个正样本,而 $(1,0,0,0)$ 是一个负样本. 首先,每个布尔变量有3种状态:0、1或不包含,因此样本空间大小为 $ |\mathcal{H}|=3^n $ .
这时,我们给出一个算法去根据样本预测原目标(具体算法略去),保证得到的假设是一致的.
那么,对于任意的 $\epsilon,\delta>0$,我们可以算出其样本复杂度:
\[m\ge \frac{1}{\epsilon}\left( n\ln3+\ln \frac{1}{\delta} \right)\]当 $\delta =0.02,\epsilon=0.1,n=10$ 时,我们可算出 $m\geq 149$.
也就是说,在至少149个样本的训练后,我们有98%的概率保证,算法习得假设的泛化误差小于 0.1,即精确度可达到 90% 以上。
3. 有限假设集上的学习保证——不一致情况
对于一致情况,我们能找到 $h_S\in \mathcal{H}$ 使得 $\widehat{R}(h_S)=0$ ,那么学习保证(Guarantees)可以由 $\mathbb{P}\left[ R\left( h_S \right) >\epsilon \right] \le \delta $ 来刻画.
对于不一致的情况,我们不一定能找到使得这样的 $h_S\in \mathcal{H}$ ,学习保证就只能由 $\mathbb{P}\left[ \left | \widehat{R}_S\left( h \right) -R\left( h \right) \right | \ge \epsilon \right] \le \delta $ 来刻画:

该推论可以直接由 Hoeffding’s inequality 得到:
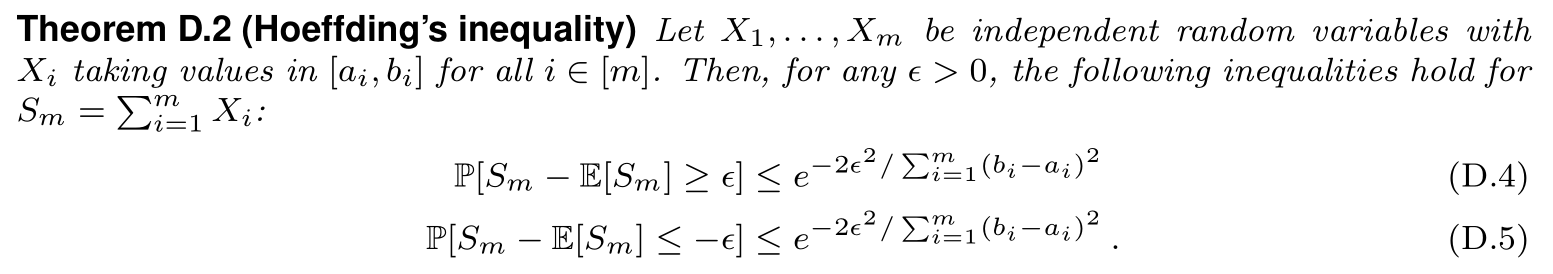
对于 0-1分类问题,我们将第 $i$ 次分类正确记为 $Y_i$,那么
\[\widehat{R}_S\left( h \right) =\frac{1}{m}\sum_{i=1}^m{Y_i},\quad R\left( h \right) =\mathbb{E}\left[ \frac{1}{m}\sum_{i=1}^m{Y_i} \right]\]注意到 $\frac{1}{m}Y_i\in \left[ 0,1/m \right] $,代入即可得证.
3.1. 学习界

从式 (2.20) 可以看出,当样本量 $m$ 增大时,误差界是在减小的,但比一致的情况要慢一些.
此外,还能看出一个在经验误差和假设集之间的权衡(trade-off):
- 假设集越大,那么拟合能力越强,经验误差就越小
- 但假设集增大的同时,本身会使误差界增大
4. 两道习题
4.1. 习题 2.3

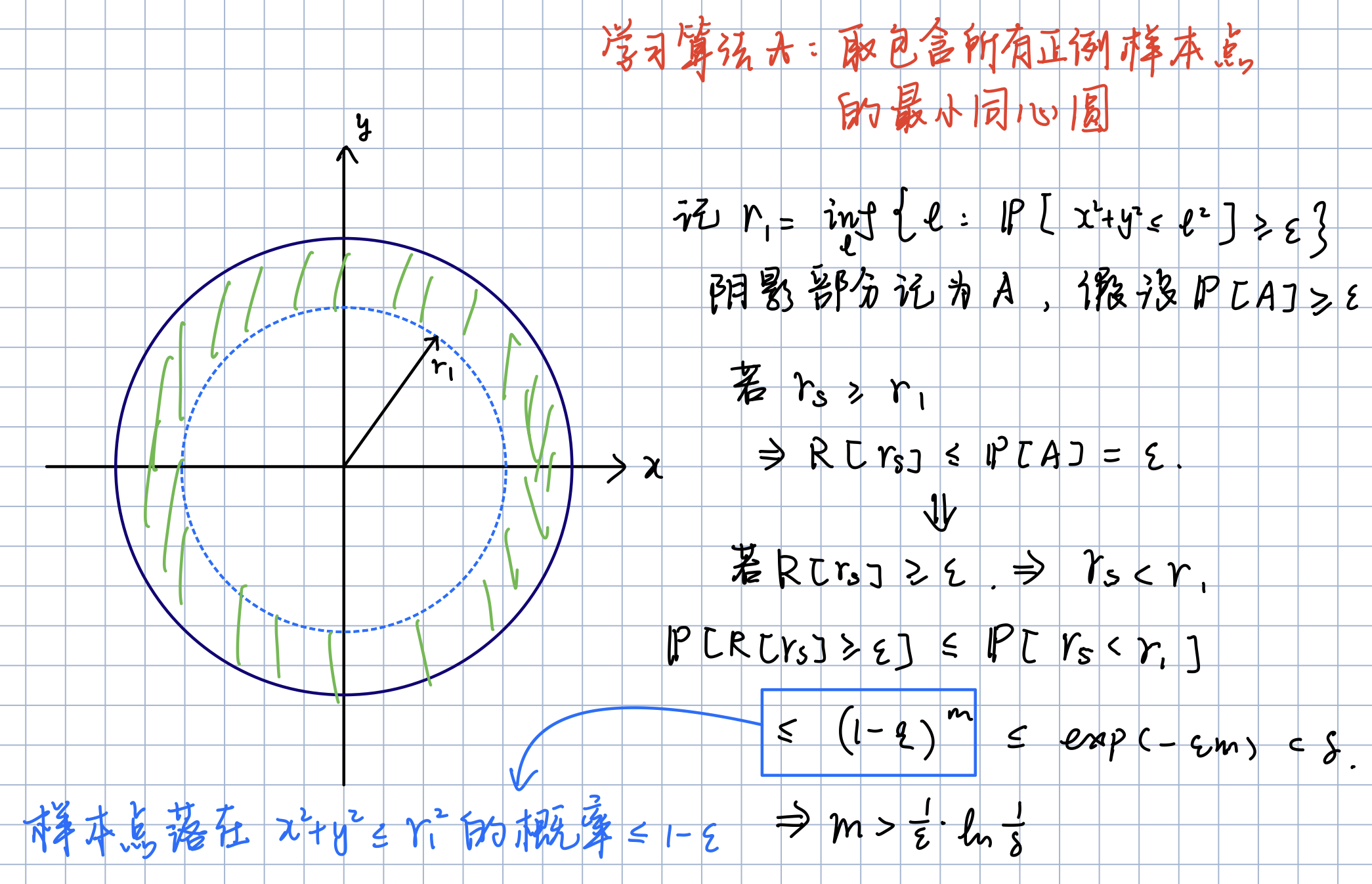
4.2. 习题2.4

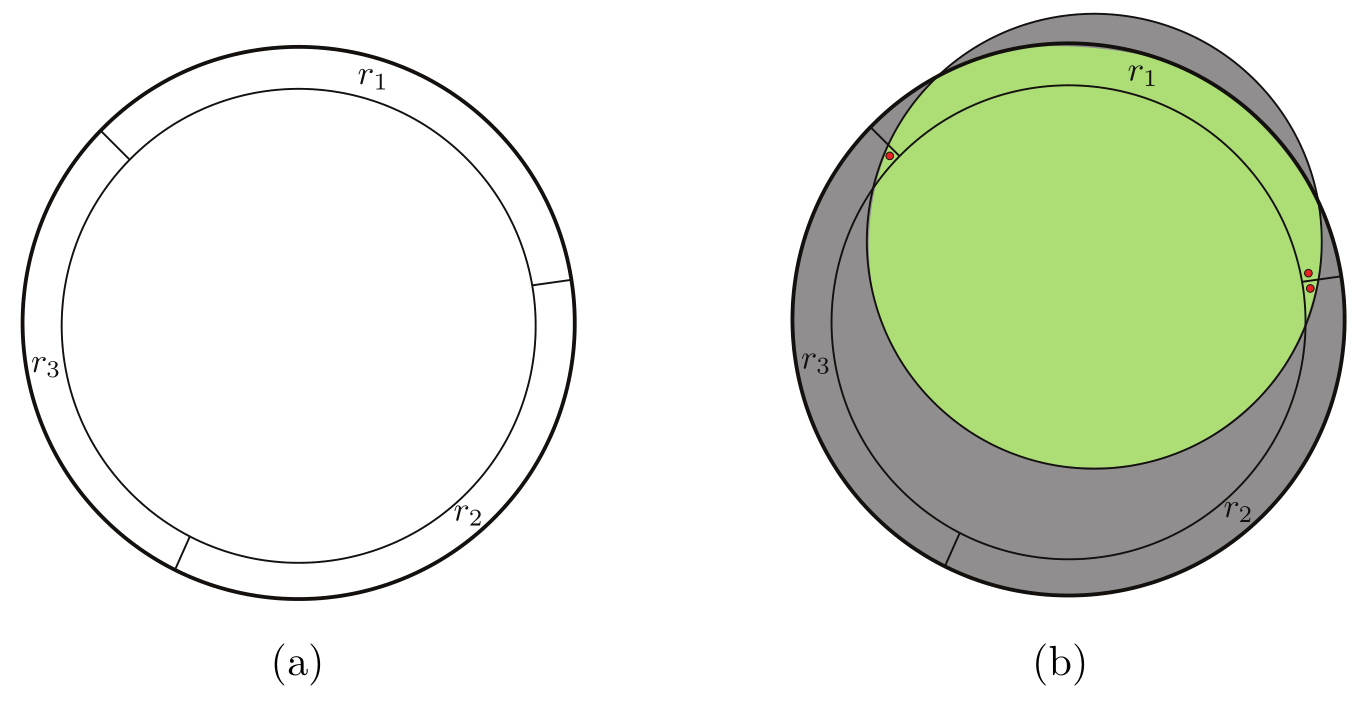
该证明的前提条件是:若学到的假设圆 $h_S$ 与 $r_1,r_2,r_3$ 都相交,那么必然有 $R(h_S)< \epsilon$.
我们知道其泛化误差就是一个样本点落在图中阴影部分的概率.
对于上一题的同心圆来说,我们知道点落在错误区域的概率一定会小于 $\epsilon$.
但对于非同心圆的情况,在已知条件仅有 $\mathbb{P}[r_i]=\epsilon/3$ 的情况下,由于不知道其他区域样本的分布情况,因此无法证明点落在阴影部分的概率小于 $\epsilon$.