三维刚体运动总结
本文参考《SLAM十四讲》,总结了刚性变化的几种表示方法。
1. 旋转矩阵
1.1. 点和坐标系
\[\mathbf{a}=\left[ \mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3 \right] \left[ \begin{array}{c} a_1\\ a_2\\ a_3\\ \end{array} \right] =a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3\]-
点 :$\mathbf{a}$
- 基:$\left(\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3 \right)$
- 坐标:$\left[ a_1,a_2,a_3 \right] ^T$
外积可以写成矩阵与向量的乘法形式:
\[\mathbf{a}\times \mathbf{b}=\left| \begin{matrix} \mathbf{e}_1& \mathbf{e}_2& \mathbf{e}_3\\ a_1& a_2& a_3\\ b_1& b_2& b_3\\ \end{matrix} \right|=\left[ \begin{array}{c} a_2b_3-a_3b_2\\ a_3b_1-a_1b_3\\ a_1b_2-a_2b_1\\ \end{array} \right] =\left[ \begin{matrix} 0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\\ \end{matrix} \right] \mathbf{b}\xlongequal{\mathrm{def}}\mathbf{a}^{\land}\mathbf{b}.\]注意:该矩阵是一个反对称矩阵:$A^T=-A$
而旋转矩阵也是一个反对称阵
\[\left[ \begin{matrix} \cos \,\theta& -\sin \,\theta\\ \sin \,\theta& \,\cos \,\theta\\ \end{matrix} \right] =\exp \left( \theta \left[ \begin{matrix} 0& -1\\ 1& \,0\\ \end{matrix} \right] \right)\]
这样就将外积转化成了线性运算。
这里引入了一个 反对称矩阵算子(skew-symetric operator),《视觉SLAM十四讲》中用 $^{\land}$ 符号来表示,它将一个向量转化成矩阵:
\[\mathbf{a}^{\land}=\left[ \begin{matrix} 0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\\ \end{matrix} \right]\]也有其他记法,例如 $\mathbf{U}=[\mathbf{u}]_\times$ ,这个更为常用。
1.2. 欧式坐标变换
\[\left[ \mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3 \right]\left[ \begin{array}{l} {a_1}\\ {a_2}\\ {a_3} \end{array} \right] = \left[ \mathbf{e}_1', \mathbf{e}_2', \mathbf{e}_3' \right]\left[ \begin{array}{l} a'_1\\ a'_2\\ a'_3 \end{array} \right].\]左边同乘一个 $\left[ \mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3 \right]^T$ \(\left[ \begin{array}{l} a_1\\ a_2\\ a_3\\ \end{array} \right] =\underbrace{\left[ \begin{matrix} \mathbf{e}_{1}^{T}\mathbf{e}_1'& \mathbf{e}_{1}^{T}\mathbf{e}_2'& \mathbf{e}_{1}^{T}\mathbf{e}_3'\\ \mathbf{e}_{2}^{T}\mathbf{e}_1'& \mathbf{e}_{2}^{T}\mathbf{e}_2'& \mathbf{e}_{2}^{T}\mathbf{e}_3'\\ \mathbf{e}_{3}^{T}\mathbf{e}_1'& \mathbf{e}_{3}^{T}\mathbf{e}_2'& \mathbf{e}_{3}^{T}\mathbf{e}_3'\\ \end{matrix} \right] }_{\mathrm{rotation} \mathrm{matrix}}\left[ \begin{array}{l} a_1'\\ a_2'\\ a_3'\\ \end{array} \right] =\mathbf{Ra}'.\)
旋转矩阵,其实就是两个标准正交基的一个张量外积。
\[\mathrm{SO}(n) = \{ \mathbf{R} \in \mathbb{R}^{n \times n} | \mathbf{R R}^T = \mathbf{I}, \mathrm{det} (\mathbf{R})=1 \}.\]$\mathrm{SO}(n)$是特殊正交群(Special Orthogonal Group)的意思。
1.3. 变换矩阵与齐次坐标
\[\left[ \begin{array}{l} \mathbf{a}'\\ 1\\ \end{array} \right] =\left[ \begin{matrix} \mathbf{R}& \mathbf{t}\\ \mathbf{0}^T& 1\\ \end{matrix} \right] \left[ \begin{array}{l} \mathbf{a}\\ 1\\ \end{array} \right] =\mathbf{T}\left[ \begin{array}{l} \mathbf{a}\\ 1\\ \end{array} \right] .\] \[\mathbf{T}^{-1}=\left[ \begin{matrix} \mathbf{R}^T& -\mathbf{R}^T\mathbf{t}\\ \mathbf{0}^T& 1\\ \end{matrix} \right] .\]这种矩阵又称为特殊欧氏群(Special Euclidean Group):
\[\mathrm{SE}(3)=\left\{ \mathbf{T}=\left[ \begin{matrix} \mathbf{R}& \mathbf{t}\\ \mathbf{0}^T& 1\\ \end{matrix} \right] \in \mathbb{R} ^{4\times 4}|\mathbf{R}\in \mathrm{SO(}3),\mathbf{t}\in \mathbb{R} ^3 \right\} .\]2. 旋转向量
任意旋转都可以用一个旋转轴 和 一个旋转角 来刻画。
于是,可以规定一个向量,其方向与旋转轴一致,长度等于旋转角。
这种向量叫旋转向量,此时变量数从9变成了3,刚好是旋转的自由度个数。
那么旋转向量怎么求呢?
2.1. Rodrigues’ rotation formula
参考 Wiki 上的 Rodrigues’ rotation formula :对于一个向量 $\mathbf{v}$ ,现在绕单位轴 $\mathbf{k}$ 做 $\theta$ 角度的旋转,那么 $\mathbf{v}_\mathrm{rot}$ 应该等于什么呢? \(\mathbf{v}_{\mathrm{rot}}=\mathbf{v}\cos \theta +(\mathbf{k}\times \mathbf{v})\sin \theta +\mathbf{k}(\mathbf{k}\cdot \mathbf{v})(1-\cos \theta )\,\)
证明懒得抄了,就参考这张图吧:
我们利用之前介绍的反对称算子 $\mathbf{U}=[\mathbf{u}]_\times$ 进行进一步的化简,我们有:
\[\mathbf{k} \times \mathbf{v} = \mathbf{K} \mathbf{v},\ \ \ \mathbf{K}=[\mathbf{k}]_\times\]再往前走一步:
\[-\mathbf{k} \times (\mathbf{k} \times \mathbf{v}) = -\mathbf{K} ^2\mathbf{v}\]那么 矩阵乘法版本 的Rodrigues公式如下:
\[R =\mathbf{I} + (1-\cos\theta)\cdot \mathbf{K}^2 + \sin \theta \cdot \mathbf{K}\]\[\mathbf{I}+[\mathbf{k}]_{\times}[\mathbf{k}]_{\times}=\mathbf{kk}^T\]这是个很神奇的定理,我想了很久没想出来,最后只能暴力证明:
若 $\mathbf{a}=\left[ \begin{array}{c} a_1
\[A^2=\left[ \begin{matrix} -a_{2}^{2}-a_{3}^{2}& a_1a_2& a_1a_3\\ a_1a_2& -a_{1}^{2}-a_{3}^{2}& a_2a_3\\ a_1a_3& a_2a_3& -a_{1}^{2}-a_{2}^{2}\\ \end{matrix} \right]\] \[A^2+I=\left[ \begin{matrix} a_{1}^{2}& a_1a_2& a_1a_3\\ a_1a_2& a_{2}^{2}& a_2a_3\\ a_1a_3& a_2a_3& a_{3}^{2}\\ \end{matrix} \right] =\mathbf{aa}^T\]
a_2
a_3
\end{array} \right]$ 为单位向量,那么有: \(A=[\mathbf{a}]_{\times}=\left[ \begin{matrix} 0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\\ \end{matrix} \right]\)
带入替换得:
\[R=\cos \theta \mathbf{I}+(1-\cos \theta )\mathbf{kk}^T+\sin \theta [\mathbf{k}]_{\times}\]取迹得 $\mathrm{tr}\left(R\right)=1+2\cos\theta$ ,即
\[\theta =\mathrm{arc}\cos \frac{\mathrm{tr}\left( R \right) -1}{2}\]旋转角 $\theta$ 已经知道了,那怎么求旋转向量 $\mathbf{k}$ 呢?
旋转向量是旋转轴,在旋转轴上进行旋转变换不会有任何改变,因此可知旋转向量 $\mathbf{k}$ 是 $R$ 的特征向量: \(R\mathbf{k}=\mathbf{k}\)
三维旋转矩阵有3个特征值,其中一个特征值为1,对应的特征向量就是旋转轴,另外两个特征值是共轭的复数。
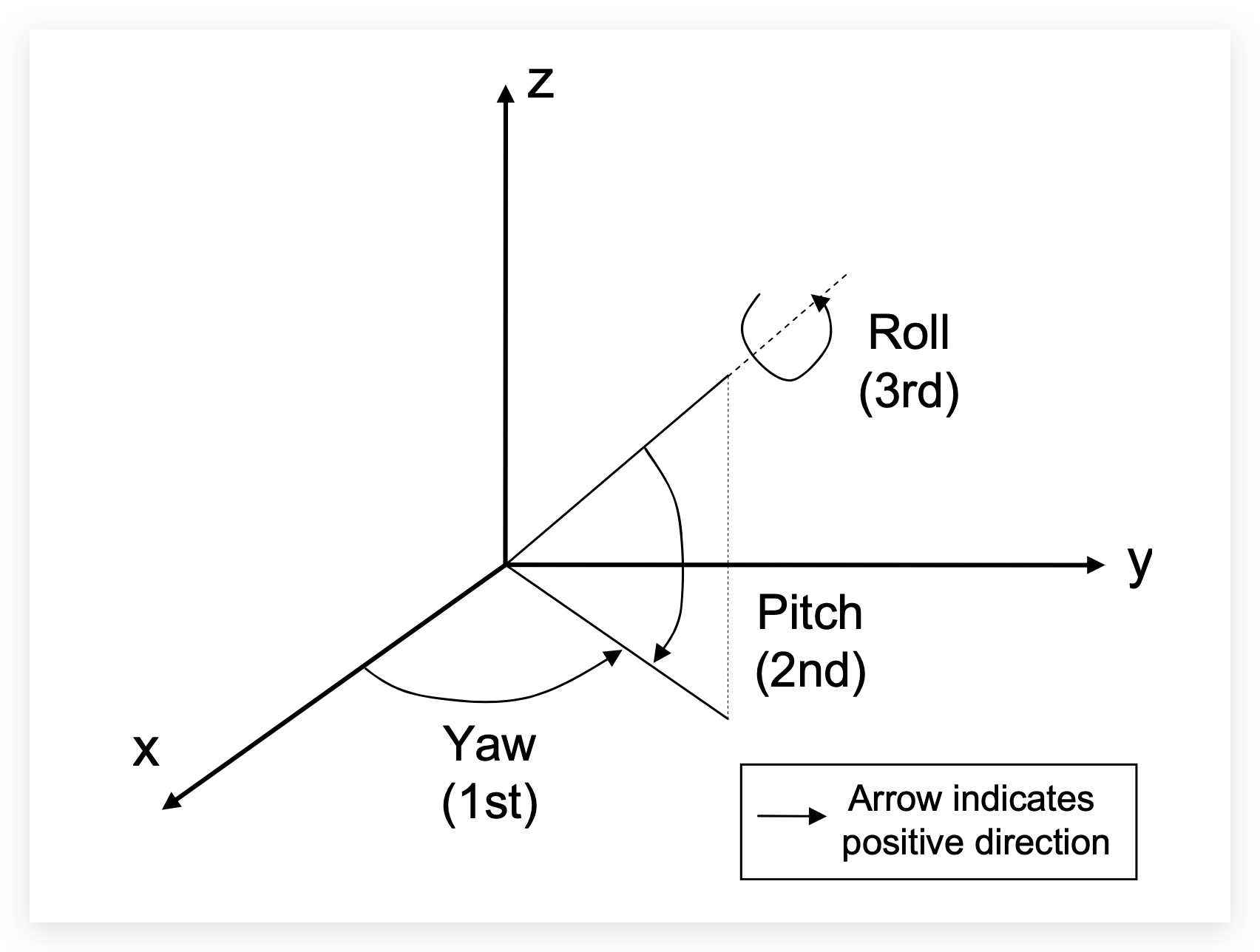
2.2. 万向锁
其实很多文章都没说清楚,其实是因为定义不清晰,放一张图就懂了。 Yaw 就是经度,Pitch 就是纬度,Roll 是绕自身旋转。 比较常见的认知错误是以为三个角都是绕坐标轴旋转,那样的话第三根轴的旋转就理解错了,单位球表面上的位置自由度为2,用不着3个变量去表示。
很明显当 Pitch 为90度时,Roll 和 Yaw 的旋转方向就重合了,失去了一个自由度,就好比你站在北极点只能朝着你面对的方向往前走,不能横着走或倒着走了一样。
3. 四元数
3.1. 定义
一个四元数$\mathbf{q}$拥有一个实部和三个虚部,像下面这样:
\[\mathbf{q} = q_0 + q_1 i + q_2 j + q_3 k\]其中$i,j,k$为四元数的三个虚部。这三个虚部满足以下关系式:
\[\left\{ \begin{array}{l} i^2=j^2=k^2=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j\\ \end{array} \right.\]也可用一个标量和一个向量来表达四元数:
\[\mathbf{q} = \left[ s, \mathbf{v} \right]^\mathrm{T}, \quad s=q_0 \in \mathbb{R},\quad \mathbf{v} = [q_1, q_2, q_3]^\mathrm{T} \in \mathbb{R}^3,\]这里,$s$ 为四元数的实部,而 $\mathbf{v}$ 为它的虚部。
可以用 单位四元数 表示三维空间中任意一个旋转,不过这种表达方式和复数有着微妙的不同:
在复数中,乘以$i$意味着旋转$90^\circ$。
而四元数中,乘以$i$对应着旋转$180^\circ$,这样才能保证$ij=k$的性质。而$i^2=-1$,意味着绕$i$轴旋转$360^\circ$后得到一个相反的东西。这个东西要旋转两周才会和它原先的样子相等。
3.2. 用四元数表示旋转
假设一个空间三维点$\mathbf{p} = [x,y,z]\in \mathbb{R}^3$,以及一个由单位四元数$\mathbf{q}$指定的旋转。
首先,把三维空间点用一个虚四元数来描述:
\[\mathbf{p} = [0, x, y, z]^\mathrm{T} = [0, \mathbf{v}]^\mathrm{T}\]那么,旋转后的点$\mathbf{p}’$即可表示为这样的乘积:
\[\mathbf{p}' = \mathbf{q} \mathbf{p} \mathbf{q}^{-1}.\]这里的乘法均为四元数乘法,结果也是四元数。最后把$\mathbf{p}’$的虚部取出,即得旋转之后点的坐标。并且,可以验证旋转后的点$\mathbf{p}’$一定为纯虚四元数。
3.3. 四元数到其他旋转表示的转换
任意单位四元数描述了一个旋转,该旋转亦可用旋转矩阵或旋转向量描述。
设 $\mathbf{q}=[s,\mathbf{v}]^\mathrm{T}$,那么,旋转矩阵 $\mathbf{R}$ 为:
\[\mathbf{R} = \mathbf{v} \mathbf{v}^\mathrm{T} + {s^2} \mathbf{I} + 2s\mathbf{v} ^ \wedge + {(\mathbf{v} ^ \wedge)}^2.\]为了得到四元数到旋转向量的转换公式,对上式两侧求迹,得:
\[\mathrm{tr}(\mathbf{R})=4s^2 -1=1+2\cos\theta\]得 旋转角:
\[\theta = 2 \arccos s\]显然有 $\mathbf{Rv}=\left( \mathbf{v}^{\mathrm{T}}\mathbf{v}+s^2 \right) \mathbf{v}=\mathbf{v}$,因此将 $\mathbf{v}$ 单位化后即可得旋转向量:
\[\mathbf{n}=\frac{\mathbf{v}}{\sqrt{1-s^2}}=\frac{\mathbf{v}}{\sin \frac{\theta}{2}}\]3.4. 小结
设四元数$\mathbf{q} = q_0+q_1i+q_2j+q_3k$,对应的旋转矩阵$\mathbf{R}$为
\[\boldsymbol{R}=\left[ \begin{matrix} 1-2q_{2}^{2}-2q_{3}^{2}& 2q_1q_2-2q_0q_3& 2q_1q_3+2q_0q_2\\ 2q_1q_2+2q_0q_3& 1-2q_{1}^{2}-2q_{3}^{2}& 2q_2q_3-2q_0q_1\\ 2q_1q_3-2q_0q_2& 2q_2q_3+2q_0q_1& 1-2q_{1}^{2}-2q_{2}^{2}\\ \end{matrix} \right]\]反之,由旋转矩阵到四元数的转换如下。假设矩阵为 $\mathbf{R}={ m_{ij}}, i, j \in \left[ 1, 2,3 \right]$,其对应的四元数 $\mathbf{q}$ 由下式给出:
\[{q_0} = \frac{\sqrt{\mathrm{tr}(R) + 1}}{2}, {q_1} = \frac{m_{23} - m_{32}}{4{q_0}}, {q_2} = \frac{m_{31} - m_{13}}{4{q_0}}, {q_3} = \frac{m_{12} - m_{21}}{4{q_0}}.\]值得一提的是,由于$\mathbf{q}$和$\mathbf{-q}$表示同一个旋转,事实上一个$\mathbf{R}$对应的四元数表示并不是唯一的。同时,除了上面给出的转换方式之外,还存在其他几种计算方法。
4. 参考
-
没那么简单——说说旋转 - 知乎 (zhihu.com)
