GNN Part 3:深入理解 GCN
为什么 GCN 能取得这么好的效果?
1. Why GCNs Work
我们知道,GCN 和 FCN 的区别就在于图卷积矩阵 $\mathrm{\hat{A}}=\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}\tilde{D}}^{-1/2}$,
\[{\color[RGB]{0, 0, 240} \mathrm{FCN}}: \mathrm{H}^{\left( l+1 \right)}=\sigma \left( \mathrm{H}^{\left( l \right)}\Theta ^{\left( l \right)} \right)\] \[{\color[RGB]{0, 0, 240} \mathrm{GCN}}: \mathrm{H}^{\left( l+1 \right)}=\sigma \left( \mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}\tilde{D}}^{-1/2}\mathrm{H}^{\left( l \right)}\Theta ^{\left( l \right)} \right)\]下面的表格是图卷积网络和全连接网络在 Cora 数据集上的结果对比,可以看到一层 GCN 的性能就已经大大超过了 FCN,而两层 GCN 的性能又有了巨大的提升。为什么仅仅乘上一个图卷积矩阵,就能取得这么好的效果提升呢?
| One-layer | Two-layer | One-layer | Two-layer |
|---|---|---|---|
| FCN | FCN | GCN | GCN |
| 0.530860 | 0.559260 | 0.707940 | 0.798361 |
1.1. Laplacian Smoothing
(Li et al., 2018) 指出,GCN 中的图卷积本质上是一种特殊的 Laplacian smoothing。
Laplace 平滑就是让一个点和它周围的点都尽可能相似,也就是让每个节点的特征都趋近于其邻域节点特征的均值。
如果加入节点自身信息的影响,即
\[\mathbf{\hat{y}}_i=(1-\gamma )\mathbf{x}_i+\gamma \sum_j{\frac{\tilde{w}_{ij}}{d_i}}\mathbf{x}_j\]其中 $0<\gamma \le 1$ 是比例参数。写成矩阵形式就是
\[\mathrm{\hat{Y}}=\mathrm{X}-\gamma \mathrm{\tilde{D}}^{-1}\mathrm{\tilde{L}X}=\left( \mathrm{I}-\gamma \mathrm{\tilde{D}}^{-1}\mathrm{\tilde{L}} \right) \mathrm{X}\]其中 $\mathrm{\tilde{L}}=\mathrm{\tilde{D}}-\mathrm{\tilde{W}}$,如果将 \(\mathrm{L}_{\mathrm{rw}}=\mathrm{\tilde{D}}^{-1}\mathrm{\tilde{L}}\) 换成 \(\mathrm{L}_{\mathrm{sym}}=\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{L}}\mathrm{\tilde{D}}^{-1/2}\),则有
\[\mathrm{\hat{Y}}=\left( \mathrm{I}-\gamma \mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{L}}\mathrm{\tilde{D}}^{-1/2} \right) \mathrm{X}\]当 $\gamma=1$ 的情况下,便得到了标准的图卷积算子:
\[\mathrm{\hat{Y}}=\left( \mathrm{I}-\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{L}\tilde{D}}^{-1/2} \right) \mathrm{X}=\left( \mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}}\mathrm{\tilde{D}}^{-1/2} \right) \mathrm{X}\]因此,图卷积可以看作一种特殊的 Laplace 平滑,使得相似的节点在特征空间中靠得更拢,这就使得分类任务更加轻松。
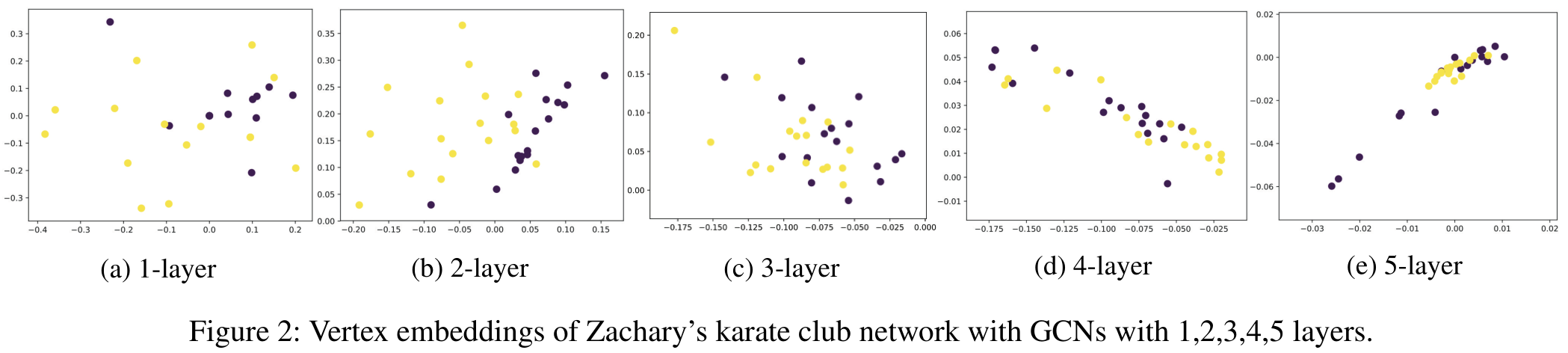
1.2. Low-pass Filter
(Wu et al., 2019) 从另一种角度来看,认为 GCN 中的图卷积本质上是一种低通滤波器。
首先,对于多层 CGN,我们先去掉非线性激活层,便得到了
\[\mathrm{\hat{Y}}=\mathrm{soft}\max \left( \mathrm{S}\cdots \mathrm{SSX}\Theta ^{(1)}\Theta ^{(2)}\cdots \Theta ^{(K)} \right)\]其中 $\mathrm{S}=\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}}\mathrm{\tilde{D}}^{-1/2}$。然后汇聚所有参数,得到一个简化版的 GCN
\[\mathrm{\hat{Y}}_{\mathrm{SGC}}=\mathrm{soft}\max \left( \mathrm{S}^K\mathrm{X}\Theta \right)\]在这里,$\mathrm{S}^K$ 是可以看作图上的一个滤波,对于 $\mathrm{S}_{\mathrm{adj}}=\mathrm{D}^{-1/2}\mathrm{WD}^{-1/2}=\mathrm{I}-\mathrm{L}$,有
\[\mathrm{S}_{\mathrm{adj}}^{K}=\left( \mathrm{I}-\mathrm{U}\Lambda \mathrm{U}^{\mathrm{T}} \right) ^K=\mathrm{U}{\color[RGB]{0, 0, 240} \left( \mathrm{I}-\Lambda \right) ^K}\mathrm{U}^{\mathrm{T}}\]该滤波的变换函数为:
\[g\left( \lambda _i \right) =\left( 1-\lambda _i \right) ^K\]如果加了自环,即
\[\mathrm{\tilde{S}}_{\mathrm{adj}}=\mathrm{I}-\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}\tilde{D}}^{-1/2}\] \[\mathrm{\tilde{S}}_{\mathrm{adj}}^{K}=\mathrm{U}{\color[RGB]{0, 0, 240} \left( \mathrm{I}-\tilde{\Lambda} \right) ^K}\mathrm{U}^{\mathrm{T}}\] \[{\color[RGB]{0, 0, 240} \text{滤波函数}}\text{: }g(\tilde{\lambda}_i ) =\left( 1-\tilde{\lambda}_i \right) ^K\](Wu et al., 2019) 证明了:添加自环会缩小谱半径。

两者特征值范围如下:
\[L=\mathrm{I}-\mathrm{D}^{-1/2}\mathrm{WD}^{-1/2}\,\, \Rightarrow \,\,\lambda _i\in {\color[RGB]{240, 0, 0} \left[ 0,2 \right] }\] \[\tilde{L}=\mathrm{I}-\mathrm{\tilde{D}}^{-1/2}\mathrm{\tilde{W}\tilde{D}}^{-1/2}\,\, \Rightarrow \,\,\tilde{\lambda}_i\in {\color[RGB]{240, 0, 0} [0,2)}\]对于不同的 $\mathrm{S}$,我们可以画出其滤波的变换函数如下:
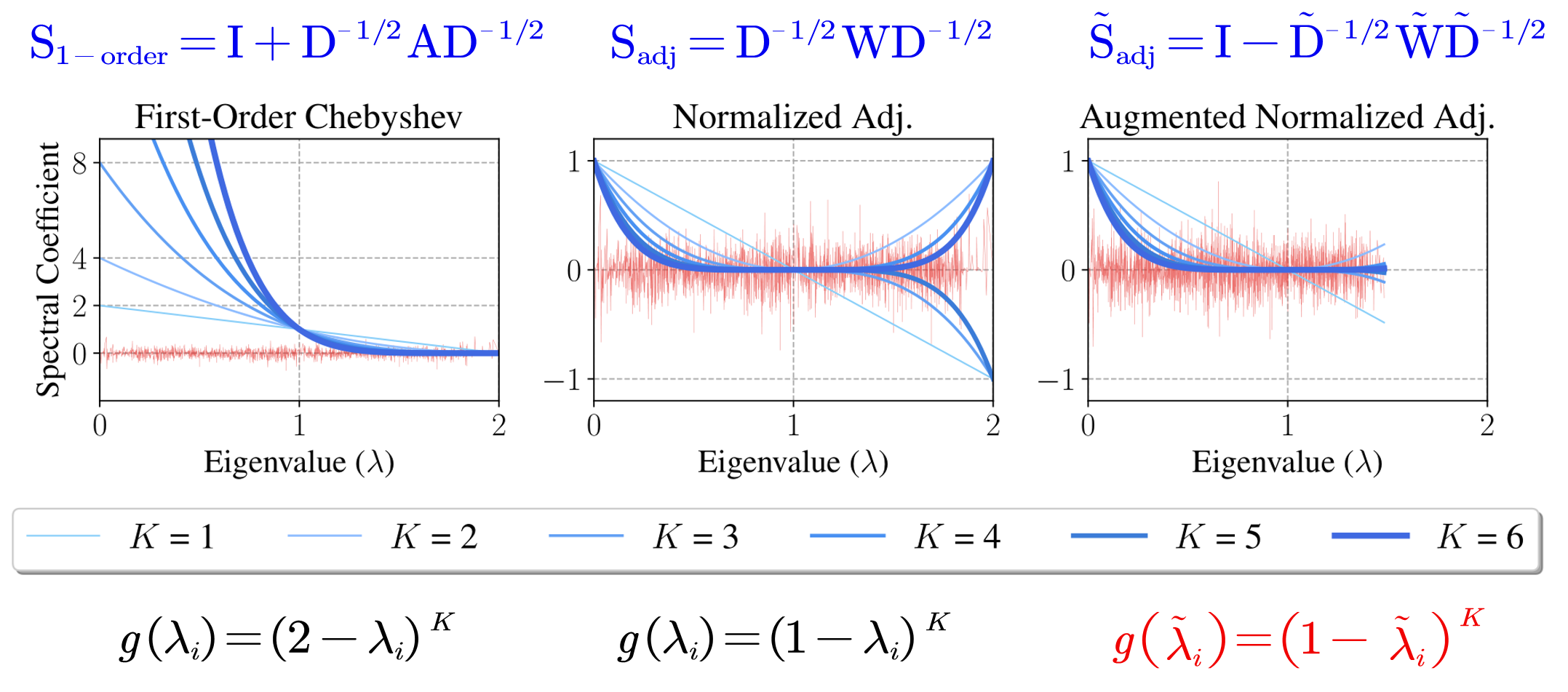
可以明显地看到,$\mathrm{\tilde{S}}_{\mathrm{adj}}$ 在低频时系数大,抑制高频信号通过,为低通滤波。
(WNT & Maehara, 2019) 对此进行了实验测试,它首先给图信号加上高斯噪声 $\mathcal{N} \left( 0,\sigma ^2 \right) $,然后只取前 $k$ 个基底重构图信号,也就是将滤波的变换函数设为截断函数,截断高频部分的图信号。 然后用这种模型训练两层神经网络,进行分类任务。
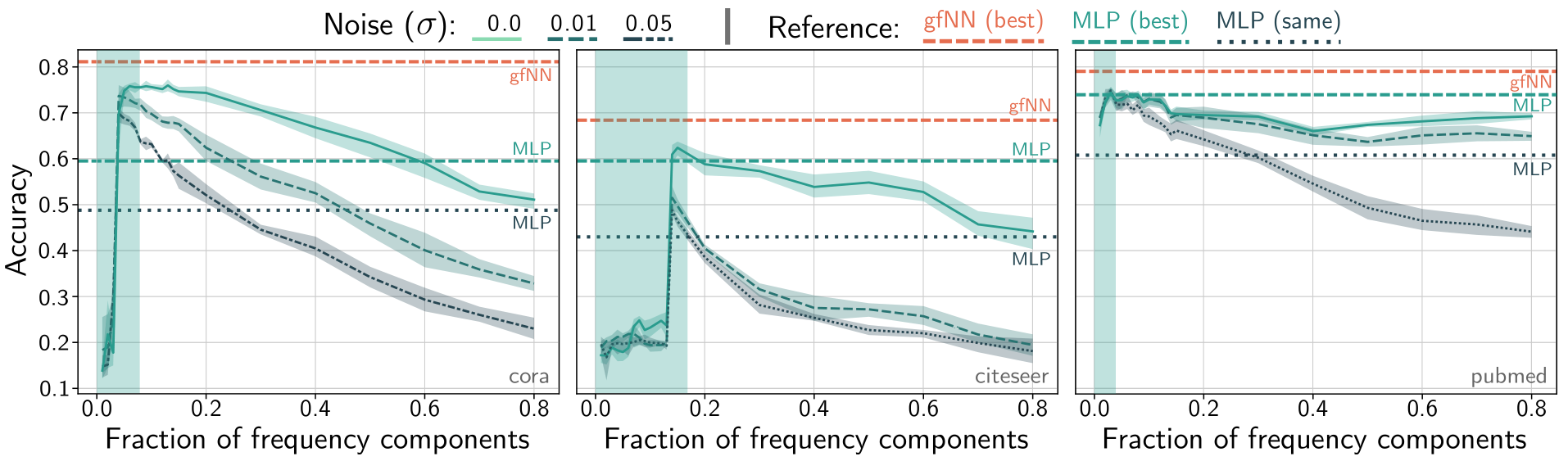
可以看到,在仅取前 20% 的低频信号时,神经网络的分类效果是最好的,高频信息的保留反而降低了分类准确率,添加的噪声越大,这种趋势就越明显,这充分说明了低通滤波器在模型中起到的作用。
2. When GCNs Fail
当然,GCN 也不是完美的,在 (Kipf & Welling, 2017) 的附录实验中,作者发现 GCN 的层数越深,分类效果反而越差。
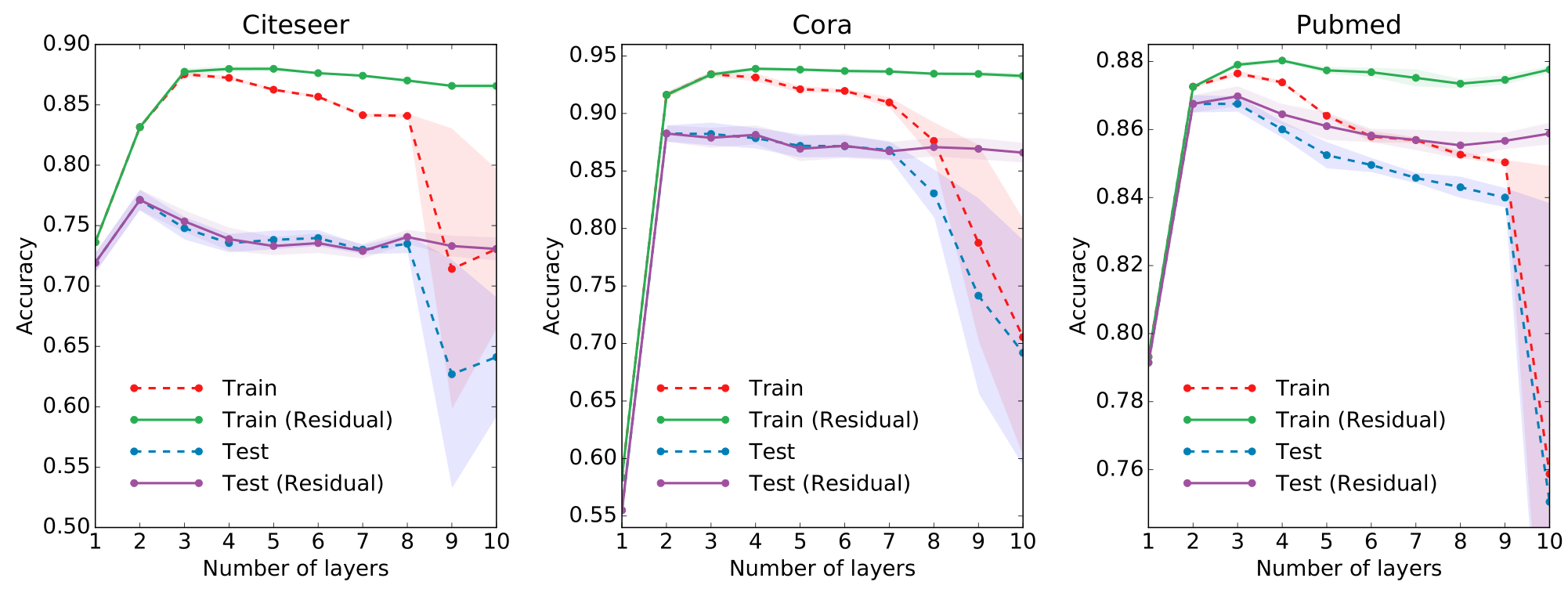
从低通滤波器的角度来说,$k$ 越大,保留的低频信息也就越少,所以当超过一定层数时分类准确率就会开始下降。
从 Laplace 平滑的角度来说,如果我们对于图信号反复做 Laplace 平滑,那么最终所有的图信号都将收敛到同一个值,节点本身的信息就全部丢失了。这也被称为过平滑 (over-smoothing) 问题。
这就使 GCN 陷入了一个两难的境地:层数深了会出现过平滑问题,但浅层 GCN 又限制了网络的表达能力。对于这个问题,(Li et al., 2018) 提出了一个解决方案:他们额外使用一个随机游走模型,然后将 GCN 和 Random Walk Model 进行协同训练 (Co-Train)。
除此之外,还有残差连接 (Skip Connection)、DropEdge 等方法。
3. Other
图神经网络博大精深,在此我也只是介绍了一些基础的 GCN 模型,还有很多基于空域的图神经网络,由于精力有限,实在是看不过来,因此先把一些值得看的论文记录下来,待有空了再来细读。
- (Xu et al., 2019) 从 Weisfeiler-Lehman 测试的角度来看 GNN 的分类能力,并以此设计了 Graph Isomorphism Network (GIN)。
- (Wu et al., 2019) 提出了一种层采用方法。
- (Ma et al., 2018) 提出了一种多视角图自编码器。
4. Reference
[1] Li, Qimai, et al. “Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning.” ArXiv:1801.07606 [Cs, Stat], Jan. 2018.
[2] Wu, Felix, et al. “Simplifying Graph Convolutional Networks.” ArXiv:1902.07153 [Cs, Stat], June 2019.
[3] NT, Hoang, and Takanori Maehara. “Revisiting Graph Neural Networks: All We Have Is Low-Pass Filters.” ArXiv:1905.09550 [Cs, Math, Stat], May 2019.
[4] Kipf, Thomas N., and Max Welling. “Semi-Supervised Classification with Graph Convolutional Networks.” ArXiv:1609.02907 [Cs, Stat], Feb. 2017.
[5] Chen, Jie, et al. “FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling.” ArXiv:1801.10247 [Cs], Jan. 2018.
[6] Xu, Keyulu, et al. “How Powerful Are Graph Neural Networks?” ArXiv:1810.00826 [Cs, Stat], Feb. 2019.
[7] Ma, Tengfei, et al. “Drug Similarity Integration Through Attentive Multi-View Graph Auto-Encoders.” ArXiv:1804.10850 [Cs, Stat], Apr. 2018.