GNN Part 2：GCN 模型

图卷积网络(Graph Convolutional Network) 借用谱图理论中图卷积的定义，在图结构的数据上定义类似 CNN 的图卷积神经网络。本文介绍了 SCNN、ChebNet 和 GCN 三种模型，从中可以看到图卷积网络的演变过程。

• 1. Spectral CNN
• 2. Chebyshev Spectral CNN
• 3. Graph Convolutional Network
• 4. GCN 实践
• 5. Reference

首先，强烈推荐阅读 Google 团队发在 Distill 上的两篇文章：

1. Understanding Convolutions on Graphs (distill.pub)
2. A Gentle Introduction to Graph Neural Networks (distill.pub)

1. Spectral CNN

在图神经网络中，我们用 $\mathbf{x}\in \mathbb{R}^{n}$ 表示图顶点上的特征向量，通过上文的介绍，我们知道特征 $\mathbf{x}$ 与滤波 $\mathbf{g}\in \mathbb{R}^{n}$ 的谱卷积定义为：

我们记 $g_{\theta}\left( \mathbf{L} \right) =\mathbf{U}\mathrm{diag}\left( \hat{g}\left( \lambda_1 \right) ,…,\hat{g}\left( \lambda _n \right) \right) \mathbf{U}^{\mathrm{T}}$，这里使用 $\theta$ 下标，表示这些元素都是神经网络中需要学习的参数。这样的话，图神经网络上的卷积操作可写作：

在 上一篇文章 中，我们使用热核函数 $\hat{g}(\lambda)=\exp(-5\lambda/\lambda_{\mathrm{max}})$ 作为卷积核，可以起到给图信号降噪的作用。但是不同场景下的需求不同，我们要怎样设计让神经网络学习 $g_{\theta}\left( \mathbf{\Lambda } \right)$ 呢？

@bruna_spectral_2014 直接将整个对角阵 $g_{\theta}\left( \mathbf{\Lambda } \right)$ 看作可学习的参数，即用参数 $\theta_1,\theta_2,\ldots,\theta_n$ 来表示 $\hat{g}\left( \lambda _1 \right) ,\hat{g}\left( \lambda_2 \right) ,…,\hat{g}\left( \lambda _n \right)$，那么卷积操作可写成：

然而这样定义的神经网络有不少缺陷：

1. 泛化能力差： 这样学到的参数 $\theta$ 与基 $\mathbf{U}$ 的相关性很强，在不同的图上，由于 $\mathbf{L}$ 不一样，生成的基 $\mathbf{U}$ 也不一样。因此该模型学到的参数只能迁移到与之同构的图上。

2. 计算量大：每次卷积操作都要乘 $\mathbf{U}$ 和 $\mathbf{U}^{\top}$，复杂度为 $\mathcal{O}(n^2)$；此外还需要对 $\mathbf{L}$ 进行显式的特征分解，其复杂度为 $\mathcal{O}(n^3)$。

3. 不具备空间局部性：传统 CNN 上的卷积都具有空间局部性(Spatial localization)：目标节点的输出是其邻域节点输入的线性组合，既能保障空间结构的学习，又能减少参数量。然而 Spectral CNN 模型中将所有的节点都参与计算，相当于一个全连接层，不具备空间局部性。

2. Chebyshev Spectral CNN

要解决 Spectral CNN 的问题很简单，其关键点就在于空间局部性，而我们在上一篇文章 GNN Part 1：谱图理论 中提到：

如果滤波函数为 $\lambda$ 的 k 阶多项式，那么该滤波具有 k 阶的空间局部性。

所以我们可以定义 $g_{\theta}\left( \mathbf{\Lambda } \right)$ 为：

卷积操作写作：

这样的话卷积核就有了空间局部性，每次只有 K-hop 邻域的节点参与卷积计算，并且将训练参数的量级从 $\mathcal{O}(n)$ 降到了 $\mathcal{O}(K)$，并且同时也避免了对矩阵 $\mathbf{L}$ 的显式特征分解。

@defferrard_convolutional_2017 提出用 Chebyshev 多项式来替换一般多项式，即定义 $g_{\theta}( \mathbf{\tilde{\Lambda} } )$ 为：

卷积操作写作：

其中 $\mathbf{\tilde{L}}=\frac{2}{\lambda _{\max}}\mathbf{L}-\mathbf{I}_n$ ，这里的 $\mathbf{L}$ 为归一化 Laplace 矩阵，其特征值范围为 $[0,2]$，那么 $\mathbf{\tilde{L}}$ 的特征值将被约束到 $[-1,1]$，因为 Chebyshev 多项式的定义域在$[-1,1]$上，此外也可以避免多层神经网络在训练时的梯度爆炸/消失现象。

Chebyshev 多项式的初项为 \(\mathrm{T}_{0}(x)=1,\,\mathrm{T}_{1}(x)=x\)， 后面项由递推式定义：

令 $\mathbf{\bar{x}}_k=\mathbf{T}_k(\mathbf{\tilde{L}})\mathbf{x},\quad\mathbf{\bar{x}}_0=\mathbf{x},\,\mathbf{\bar{x}}_1=\mathbf{\tilde{L}x}$，然后可通过递推计算：

那么卷积操作可写成

由于 $\mathbf{L}$ 是稀疏矩阵，计算复杂度可降到 $\mathcal{O}(mK)$。

我一直有一个很大的问题：

为什么要用 Chebyshev 多项式来代替一般多项式？

很多文章说是用递推的方式可以节省计算量，但 Chebyshev 多项式相当于把 \(\mathbf{\bar{x}}_k=2\mathbf{\tilde{L}\bar{x}}_{k-1}-\mathbf{\bar{x}}_{k-2}\) 替换成 \(\mathbf{\bar{x}}_k=\mathbf{\tilde{L}\bar{x}}_{k-1}\)​，两者计算复杂度是一模一样的。而原论文也没有提到相比于传统多项式， Chebyshev 多项式的优势在哪。 我上网找了很多关于这篇论文的解读，都没有解释清楚这个问题，最后终于在 GitHub 的 issues #35 中找到了答案：作者很诚实地回复说其实没啥区别。。。

我四十米的大刀差点就收不回去了，还好作者勉强找了个理由糊弄我们：Chebyshev 多项式比一般多项式的正交性好那么一丢丢，所以当一个系数被扰动时，其他系数所受到的影响更小，也就是可能具有更好的稳定性。然后有人问 Legendre 多项式的正交性更强你为啥不用它呢？作者说因为我们对 Chebyshev 多项式更熟悉一点，但实际上不管是一般多项式还是 Legendre 多项式，它们都没啥区别。。。(我只想说作者你这么诚实真的很容易被打)

Why the Chebyshev polynomials is needed? · Issue #35 · mdeff/cnn_graph (github.com)

Q: I don’t know why the Chebyshev is needed?

A: Any polynomial (monomials, Chebyshev, Legendre, etc.) of order K has the same representation power and can be used. We used Chebyshev because we had experience with it and thought it would be easier to optimize as they form an orthogonal basis. There’s however not much difference in practice.

Chebyshev polynomials are more orthogonal (under the identity measure, and truly orthogonal with measure 1/sqrt(1-x²)) than monomials, but less than Legendre (truly orthogonal with the identity measure).

In the vertex domain (for a ring/circle graph), Chebyshev and Legendre polynomials are also more orthogonal than monomials.

Q: Why did you choose the Chebyshev Polynomials of first kind instead of the Legendre Polynomials?

A: Mostly for historical reasons. At first we were designing filters (e.g., to solve the diffusion of heat, the propagation of waves, and many others). As Chebyshev polynomials are excellent function approximators, we chose them to approximate those ideal filters we wanted to design. When learning filters, the choice of a polynomial basis doesn’t matter for the expressivity of the filters, so we kept Chebyshev as we were familiar with them. We thought it could be easier to optimize, but that doesn’t seem to make a difference in practice.

3. Graph Convolutional Network

@kipf_semi-supervised_2017 在 ChebNet 的基础上继续简化：首先设置 $K=1$，将感受野限制在 1-hop 邻域，类似于 CNN 中的 $3\times3$ 卷积， 然后使用近似 $\lambda_{\mathrm{max}}\approx 2$，式 $\eqref{eq:chev}$ 可简化为：

这里有两个参数 $\theta_{0}^{\prime}$ 和 $\theta_{1}^{\prime}$，原论文认为需要减少参数量以避免过拟合，所以设置 $\theta =\theta_{0}^{\prime}=-\theta_{1}^{\prime}$，得到新的表达式：

由于 $\mathbf{I}_n+\mathbf{D}^{-\frac{1}{2}}\mathbf{WD}^{-\frac{1}{2}}$​ 的特征值范围为 $[0,2]$​，为了避免梯度爆炸或梯度消失，作者提出了 重归一化技巧(Renormalization trick)：

其中 \(\mathbf{\tilde{W}}=\mathbf{W}+\mathbf{I}_n,\,\mathbf{D}_{ii}=\sum_j{\mathbf{\tilde{W}}_{ij}}\)，得到最终的表达式：

Renormalization trick 有什么用呢？

在我看来，最主要的作用就是将矩阵特征值的范围重新限制到了区间 $(-1,1]$ 中。而另一方面，增加了一个 $\mathbf{I}_n$ 可以看作添加了节点本身的信息，于是不妨将这个自身信息放到邻接矩阵中，等价于加了个自环，然后 $\mathbf{\tilde{D}}^{-\frac{1}{2}}\mathbf{\tilde{W}\tilde{D}}^{-\frac{1}{2}}$ 则是对这个自信息也进行了归一化。

4. GCN 实践

我们使用作者的 pytorch 代码实现：tkipf/pygcn: GCN in PyTorch (github.com)。

首先数据集为 cora 数据集，该数据集是一个论文图，共 2708 个节点，1433 条边，每个节点都是一篇论文，论文的特征是通过词袋模型得到的，维度为 1433，每一维代表一个词，1 表示这个词在文章中出现过，0 代表未出现。所有论文根据主题被分为 7 类，论文图中的每一条边代表一篇论文引用了另一篇论文。

实验中使用了 140 个节点的标签进行训练，然后用训练好的模型来预测剩下节点的标签，这也是标题中包含了“半监督分类”(Semi-supervised classification)的原因。

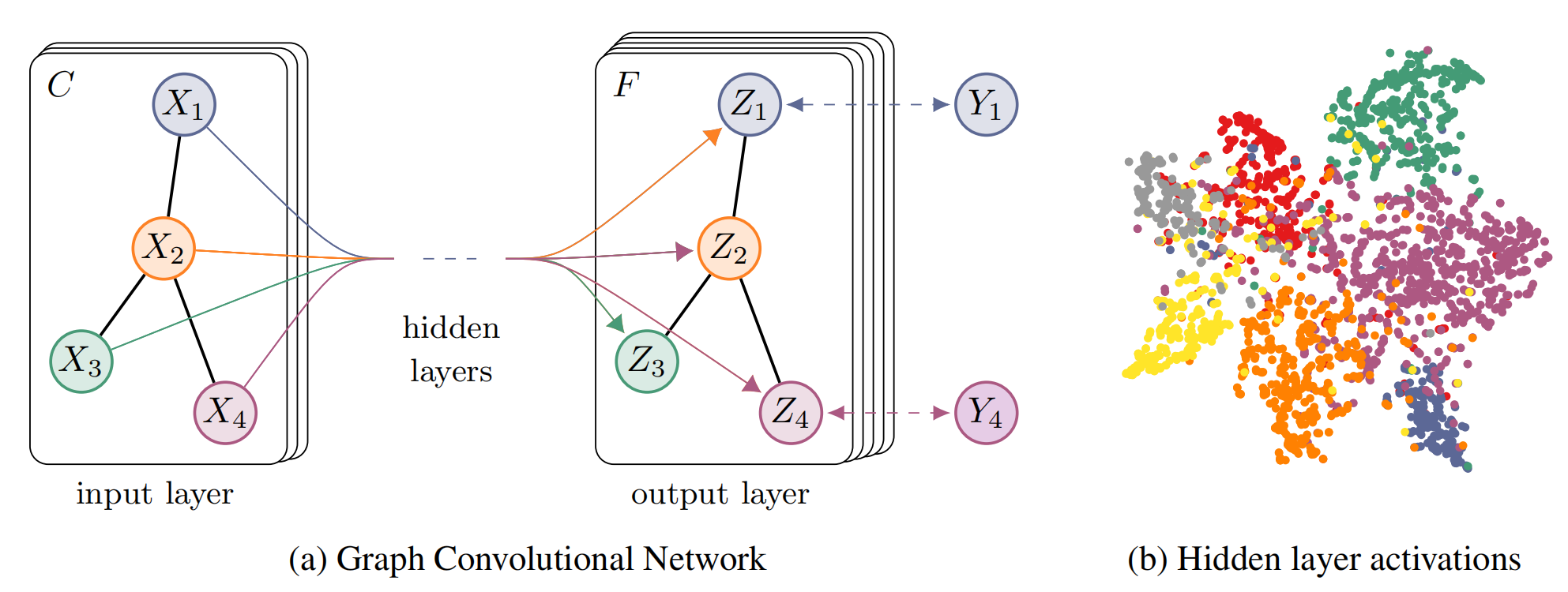
模型的网络结构为双层 GCN，输出层使用 softmax 将特征转化为类别概率。

其中 $\mathbf{\hat{A}}=\mathbf{\tilde{D}}^{-\frac{1}{2}}\mathbf{\tilde{W}\tilde{D}}^{-\frac{1}{2}}$。

最后 loss 采用交叉熵函数 ：

核心代码如下：

class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

其中 GraphConvolution() 就是稀疏矩阵的乘法，adj 就是重归一化后的邻接矩阵 $\mathbf{\hat{A}}$。注意到作者中间还使用了个 dropout 层，最后的实验结果如下：

Epoch: 0195 loss_train: 0.3925 acc_train: 0.9357 loss_val: 0.7099 acc_val: 0.8067 time: 0.0100s
Epoch: 0196 loss_train: 0.4266 acc_train: 0.9643 loss_val: 0.7093 acc_val: 0.8033 time: 0.0090s
Epoch: 0197 loss_train: 0.4399 acc_train: 0.9286 loss_val: 0.7083 acc_val: 0.8033 time: 0.0090s
Epoch: 0198 loss_train: 0.4568 acc_train: 0.9357 loss_val: 0.7071 acc_val: 0.8033 time: 0.0100s
Epoch: 0199 loss_train: 0.4535 acc_train: 0.9429 loss_val: 0.7046 acc_val: 0.8000 time: 0.0087s
Epoch: 0200 loss_train: 0.4246 acc_train: 0.9143 loss_val: 0.7033 acc_val: 0.8000 time: 0.0100s
Optimization Finished!
Total time elapsed: 3.3199s
Test set results: loss= 0.7386 accuracy= 0.8260

可以看到，在只使用了 5% 节点标签的情况下，模型训练了 200 步就能达到 82% 的准确率，这个效果是相当不错的。

5. Reference

[1] Bruna, Joan, et al. “Spectral Networks and Locally Connected Networks on Graphs.” ArXiv:1312.6203 [Cs], May 2014.

[2] Defferrard, Michaël, et al. “Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering.” ArXiv:1606.09375 [Cs, Stat], Feb. 2017.

[3] Kipf, Thomas N., and Max Welling. “Semi-Supervised Classification with Graph Convolutional Networks.” ArXiv:1609.02907 [Cs, Stat], Feb. 2017.