黎曼流形上的优化方法
对于一些特殊的约束优化问题,其约束具有流形结构(例如 SO(3) 约束),那么我们可以将欧式空间中的约束优化问题看做流形上的无约束优化问题。此文章有 LaTeX 版,点击 manopt.pdf 即可下载。
1. Introduction
1.1. 问题描述
对于两个 $\mathbb{R}^3$ 中的对应点集 \(\mathcal{P}=\left\{ p_1, p_2,\ldots, p_n \right \}\) 和 \(\mathcal{Q}=\left\{ {q}_{1}, {q}_{2}, \ldots, {q}_{n}\right\}\),我想找到一个旋转变换使得两个点集在 L1 范数的意义下配准(对于一般的点云配准来说,此处还需要平移变换,但为简化起见这里省略)。用数学方式来表示,就是想找到一个旋转矩阵 $R^{\star}$ 使得:
\[R^{\star}=\underset{R\in \mathrm{SO}(3)}{\mathrm{arg}\min}\sum_{i=1}^n\left\| Rp_i-q_i \right\| _1\]矩阵 $R$ 如果属于旋转矩阵 $\mathrm{SO}(3)$,则需要满足的条件为:
\[R R^T=I_3,\det(R)=1\]可将其写成矩阵的形式
\[R^{\star}=\underset{R\in \mathrm{SO(}3)}{\mathrm{arg}\min}\left\| RP-Q \right\| _1\]其中 \(P=[{p}_{1}, {p}_{2}, \ldots, {p}_{n}]\in \mathbb{R}^{3\times n},Q=[{q}_{1}, {q}_{2}, \ldots, {q}_{n}]\in \mathbb{R}^{3\times n}\)。 这里的 \(\|\cdot\|_1\) 表示矩阵所有元素的绝对值之和。
1.2. 流形优化介绍
如果没有 $\mathrm{SO}(3)$ 这个约束条件,那么我们可以直接计算目标函数的次梯度,然后使用梯度下降方法求解即可。
\[f(R)=\left\| RP-Q \right\| _1\] \[\nabla _Rf=\mathrm{sign(}RP-Q)\cdot P^{\top}\]但问题在于我们的 $R$ 需要满足 $\mathrm{SO}(3)$ 约束,单纯使用梯度下降并不能保证满足约束条件。但幸运的是, $\mathrm{SO}(3)$ 是欧式空间 $\mathbb{R}^9$ 中的光滑子流形,我们可以将每一步的迭代点都限制在流形上,然后就可以在流形空间中使用那些无约束优化方法了,这就是流形优化。
直观的解释可以参考下图,假设约束流形为 $\mathcal{M}$ ,已知当前迭代点为 $x_k$,我们先计算目标函数在欧式空间的梯度 $-\nabla f(x_k)$,但新迭代点 $x_k-\nabla f(x_k)$ 不一定在流形 $\mathcal{M}$ 上,因此我们需要考虑如何构造一个合适的映射,将欧式空间的中的点映射到 $\mathcal{M}$ 。
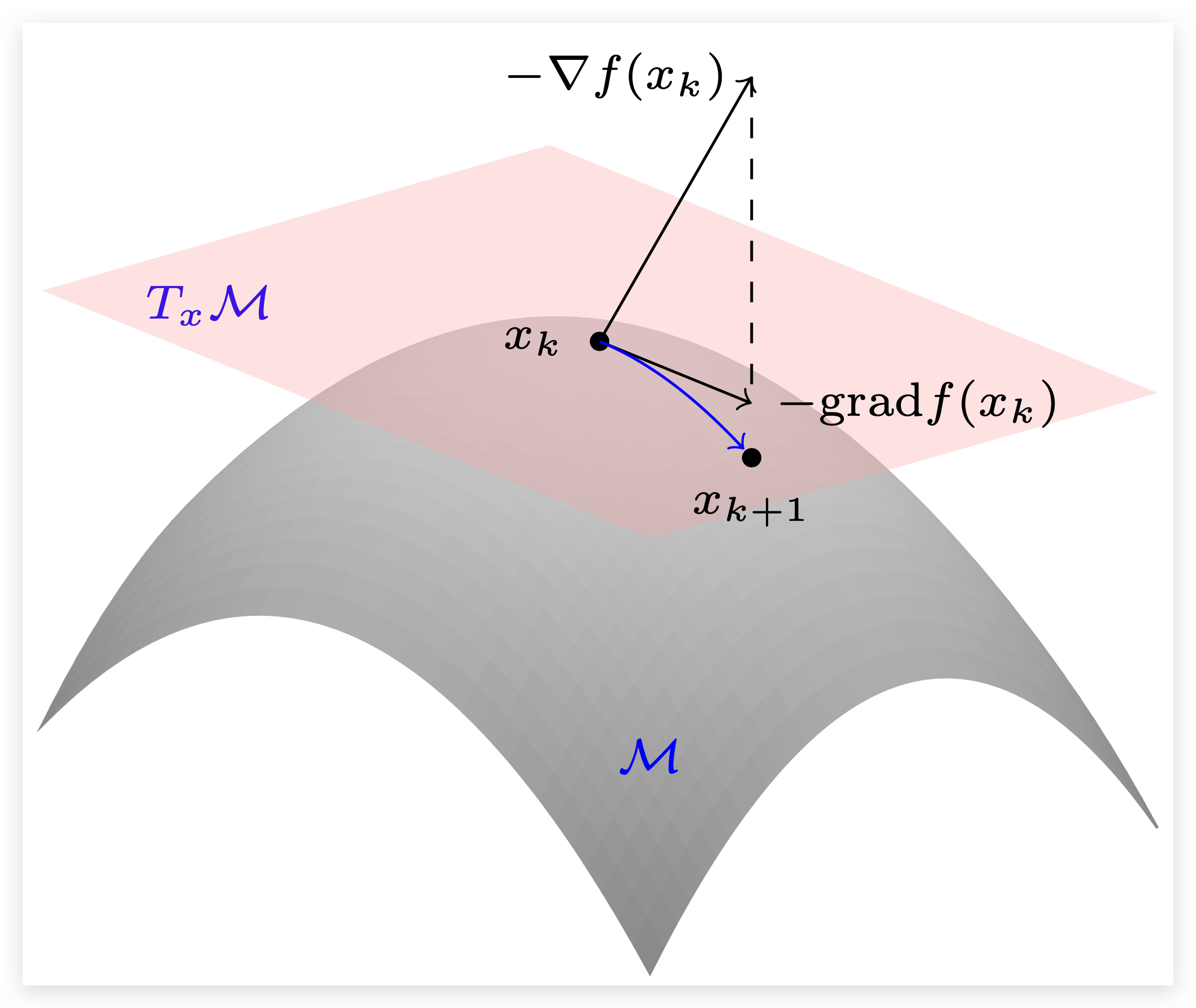
首先考虑到切空间 $T_{x_k}\mathcal{M}$ 是流形 $\mathcal{M}$ 在点 $x_k$ 处的线性近似,因此一个很自然的想法就是先将欧式空间的点投影到切空间 $T_{x_k}\mathcal{M}$ 上,然后再将 $T_{x_k}\mathcal{M}$ 上的点映射到 $\mathcal{M}$ ,这样就完成了一次黎曼梯度下降。常规的拟牛顿法、信赖域法等优化方法都能拓展到流形优化中。
现在我们大体思路已经明确,接下来就是具体计算每一步的变换。若只是快速上手应用,那么直接套公式即可,但如果想弄清楚公式的每一步是怎么来的,那么还需要一些黎曼几何的基础知识。
2. 黎曼几何基础
2.1. 切向量
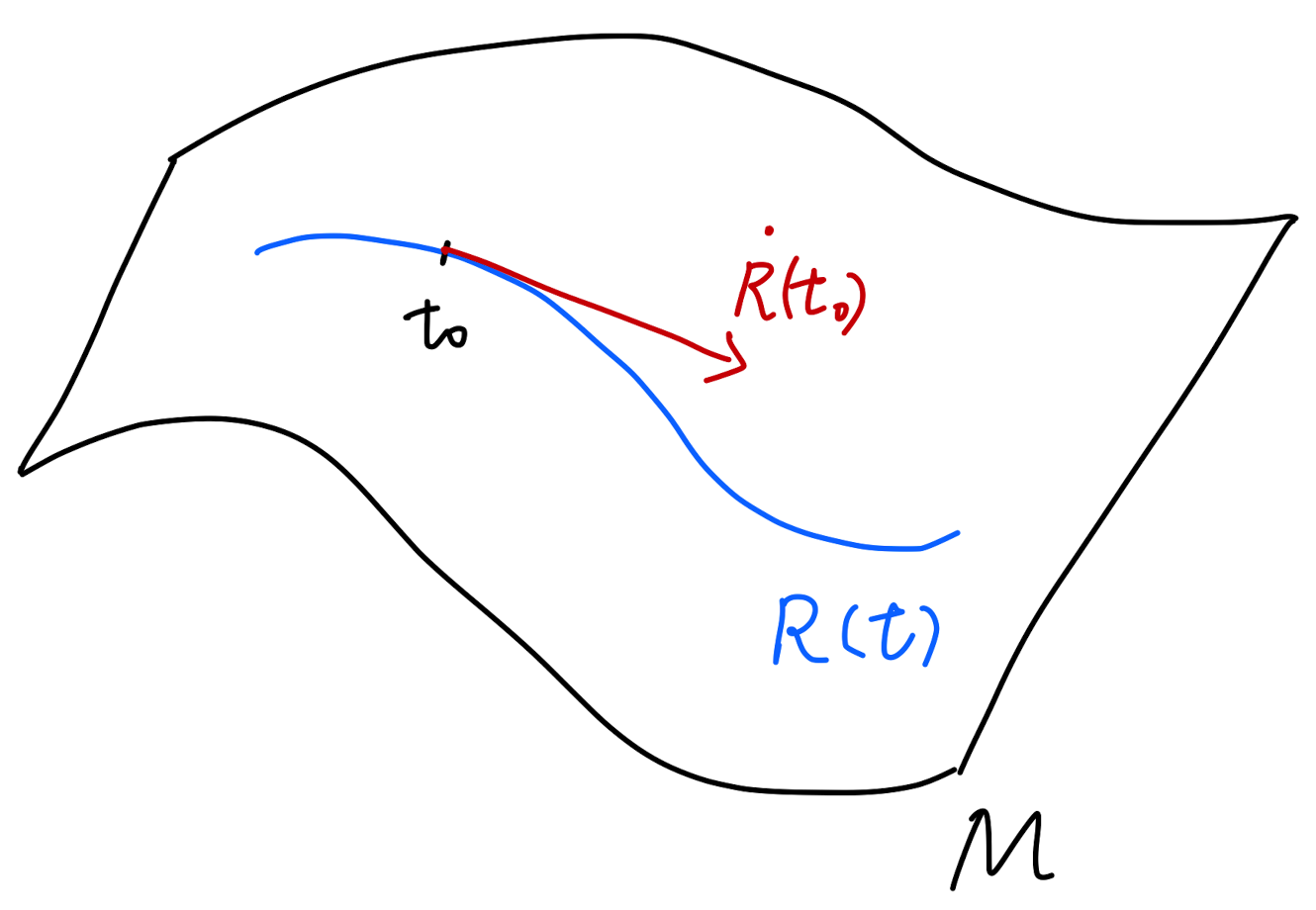
$R(t)$ 是定义在 $\mathrm{SO}(3)$ 上的一条光滑曲线,如果 $R(t_0)=A$,那么 $H=\dot{R}(t_0)$ 就是点 $A$ 处的一个切向量。 由于 $R(t)^TR(t)=I$ ,于是有:
\[\dot{R}(t)^T{R}(t)+R(t)^T\dot{R}(t)=0\]也就是说在$\mathrm{SO}(3)$流形中,点$A$ 处的切向量$H$ 需要满足$H^TA+A^TH=0$。
2.2. 切空间
所有曲线在点 $A$ 处的切向量构成一个切空间 $T_A\mathrm{SO}(3)$ ,其定义为:
\[T_A\mathrm{SO}(3) =\{H:H^TA+A^TH=0\}\]设$\Omega=A^TH$,那么也可写成:
\[T_A\mathrm{SO}(3) =\{A\Omega:\Omega+\Omega^T=0\}\]注意此处的 $\Omega$ 是一个反对称矩阵。我们知道每一个旋转矩阵都能表示为一个反对称矩阵的指数映射,而此处点$A$ 所对应的反对称矩阵恰恰就是$\Omega$,这一点我们会在后面提到。
2.3. 内积
在定义了切空间后,我们需要在流形的切空间上定义内积。 欧式空间中内积的定义为 $\left< a,b \right> =a^Tb$ ,很自然地,我们可以将该定义沿用到子流形$\mathrm{SO}(3)$上,切空间 $T_X\mathrm{SO}(3)$ 上的内积可定义为
\[\left< A,B \right> _X:=\operatorname{vec}(A)^T\operatorname{vec}(B)=\mathrm{tr}\left( A^TB \right)\]在切空间中定义了内积后,自然便有了黎曼度量, 该流形也就可以称作黎曼流形了。
2.4. 方向导数
对于光滑的实值函数$f:\mathrm{SO}(3)\rightarrow\mathbb{R}$, 我们可以在切空间上定义$f$ 沿着切向量$H \in T_X\mathrm{SO}(3)$ 的方向导数:
\[\mathrm{D}f(X)\left[ H \right] =\lim_{t\rightarrow 0}\dfrac{f(X+tH)-f(X)}{t}\]2.5. 黎曼梯度
对于黎曼流形 $\mathcal{M}$ , 函数$f$ 在$x$ 点处的黎曼梯度$\mathrm{grad} f(x)$ 是$T_x\mathcal{M}$ 中的一个向量,由条件 $\eqref{rmgrad}$ 唯一确定。
\[\left< \mathrm{grad} f(x),\xi \right> _x=\mathrm{D}f(x)\left[ \xi \right] ,\quad \forall \xi\in T_x\mathcal{M} \tag{1} \label{rmgrad}\]黎曼梯度的方向也是使方向导数最大化的方向。
由于$\mathrm{SO}(3)$ 是欧式空间中的黎曼子流形,因此其黎曼梯度就是欧式空间中的梯度$\nabla f(X)$ 在切空间 ${T_X\mathrm{SO}(3)}$ 上的投影:
\[\mathrm{grad}f(X)=\mathcal{P}_{T_X\mathrm{SO}(3)}\left( \nabla f(X) \right)\]投影的计算公式为:
\[\mathcal{P}_{T_X\mathrm{SO}(3)}\left( M \right)=X\mathrm{skew}\left( X^TM \right),\]其中 $\mathrm{skew}$ 是反对称算子:$\mathrm{skew}\left( A \right) =\frac{A-A^T}{2}$。
最终算得:
\[\begin{aligned} \mathrm{grad}f(X)&=\frac{1}{2} \left(\nabla f(X) -X\nabla^T f(X)X\right)\\ &=\nabla f(X)-X\mathrm{sym} \left(X^T\nabla f(X)\right) \end{aligned}\]其中 $\mathrm{sym}(A)=\frac{A+A^T}{2}$。
2.6. 黎曼 Hessian
对于黎曼流形 $\mathcal{M}$ 上的实值函数 $f:\mathcal{M} \rightarrow \mathbb{R}$ ,给定黎曼联络 $\tilde{\nabla}$ ,可计算其黎曼 Hessian:
\[\mathrm{Hess}f\left( x \right) \left[ \xi \right] := \tilde{\nabla}_{\xi}\mathrm{grad}f\left( x \right) ,\quad \xi \in T_{x}\mathcal{M}\]同样的,要计算$\mathrm{SO}(3)$ 的黎曼 Hessian,只需将其黎曼梯度在欧式空间中的方向导数投影到切空间上即可:
\[\begin{aligned} \mathrm{Hess}f\left( X \right) \left[ U \right] & =\mathcal{P} _{T_X\mathrm{SO}\left( 3 \right)}\left( D\mathrm{grad}f\left( X \right) \left[ U \right] \right) \\ & =\mathcal{P} _{T_X\mathrm{SO}\left( 3 \right)}\left( \nabla ^2f\left( X \right) \left[ U \right] -U\mathrm{sym}\left( X^T\nabla f\left( X \right) \right) -XS\right)\\ & =\mathcal{P} _{T_X\mathrm{SO}\left( 3 \right)}\left( \nabla ^2f\left( X \right) \left[ U \right] -U\mathrm{sym}\left( X^T\nabla f\left( X \right) \right) \right)\end{aligned}\]其中 $S= \mathrm{sym}\left( U^T\nabla f\left( X \right) +X^T\nabla ^2f\left( X \right) \left[ U \right]\right)$ ,$U \in T_X\mathrm{SO}(3)$ ,可算出 $XS$ 在切空间上的投影为0。
2.7. 测地线
测地线是黎曼流形上连接两点之间的最短曲线,并且测地线的沿曲线加速度$\gamma ‘‘\left( t \right)$ 恒为0。沿曲线加速度可以通过曲线在欧式空间中加速度的投影得到:
\[\gamma ''\left( t \right) =\mathcal{P} _{T_{\gamma \left( t \right)}\mathcal{M}}\left( \ddot{\gamma}\left( t \right) \right)\]也就是说,测地线在欧式空间中的加速度方向与切空间垂直。
2.8. 指数映射
我们现在要计算切空间$T_x\mathcal{M}$到流形$\mathcal{M}$上的映射$f$ ,一个很自然的想法就是将切向量$v$ 投影到流形上,那么哪些条件需要被满足呢?首先,切空间的原点必须映射到切点,即$f(0)=x$;然后直线$vt$ 在流形上的投影必然是一条测地线 $r(t)$;如果切向量$v$的长度变成了原来的$a$ 倍,那么测地线的长度也应该要增大到原来的$a$ 倍。我们将上面这些要求整理之后,得到如下条件:
对于黎曼流形 $\mathcal{M}$上的一个点 $x$ ,给定$x$ 点处的一个切向量$v$ ,寻找满足以下3个条件的测地线 $\gamma(t)$:
-
$\gamma(0)=x$
-
$\dot{\gamma}(0)=v$
-
$\gamma(at;x,v)=\gamma(t;x,av)$
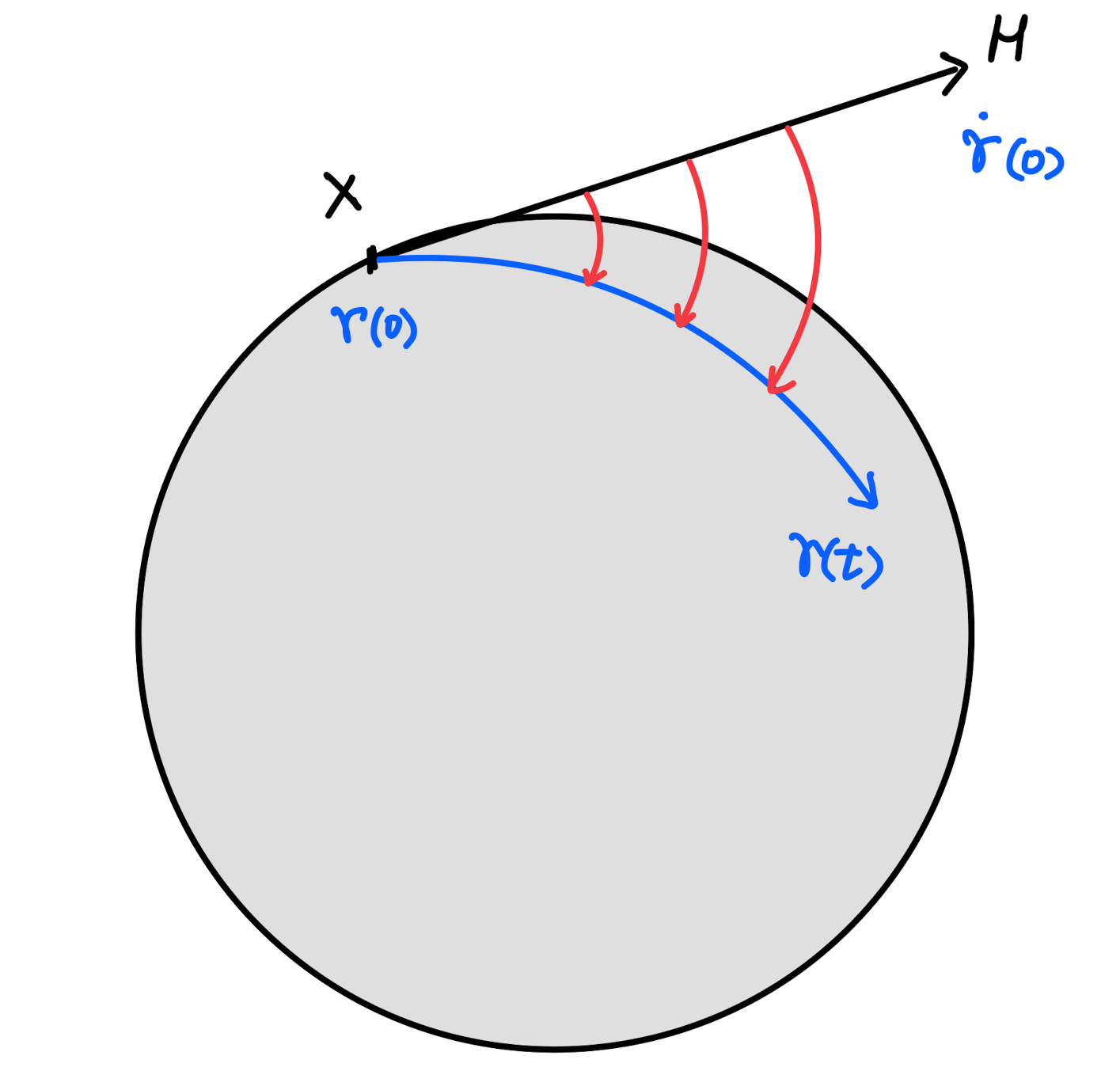
那么可以定义从切空间$T_x\mathcal{M}$ 到流形$\mathcal{M}$ 上的映射:
\[\mathrm{Exp}\left( x,v \right) =\mathrm{Exp}_x\left( v \right) =\gamma \left( 1;x,v \right)\]该映射就称为在$x$ 点处的指数映射。
对于$\mathrm{SO}(3)$ 流形,以$X$ 为起点,沿切向量$H$ 方向延伸的测地线方程如下,具体推导过程见附录。
\[\gamma \left( t \right) =X\exp \left( tX^TH \right)\]由此可知$\mathrm{SO}(3)$ 在$X$ 处的指数映射为:
\[\mathrm{Exp}_X\left( H \right) =X\exp \left( X^TH \right)\]2.9. 对数映射
对数映射从流形映射到切空间,是指数映射的逆,$\mathrm{SO}(3)$ 在$X$ 处的对数映射为:
\[\mathrm{Log}_X\left( Y \right) =X\log \left( X^TY \right)\]2.10. 测地距离
对于点$Y$,若$\mathrm{Log}_X\left( Y \right)=V$,那么有$\mathrm{Exp}_X\left( V \right) =Y$,我们可以写出 $X$ 到 $Y$ 的测地线方程:
\[\gamma(t)=X\exp\left( tX^TV \right)\]其中 $\gamma(0)=X,\gamma(1)=Y$, 那么$X$ 到 $Y$ 的测地距离为:
\[\begin{aligned} \mathrm{dist}(X,Y)&= \int_0^1\|\gamma'(t)\|_{\gamma(t)}\,\mathrm{d}t\\ &=\int_0^1\|\gamma(t)X^TV\|_{\gamma(t)}\,\mathrm{d}t\\ &=\int_0^1\|V\|_{\gamma(t)}\,\mathrm{d}t\\ &=\|V\| \end{aligned}\]由此可见 $V$ 的模长 \(\|V\|\) 就是 $X$ 到 $Y$ 的测地距离。
我们闲得无聊可以继续往下算,先设 $\exp \left(\theta [n]_{\times} \right)=X^TY$,那么有:
\[\begin{aligned} \mathrm{dist}(X,Y)^2&= \left<X\theta [n]_{\times} ,X\theta [n]_{\times} \right>\\ &= \theta^2 \mathrm{tr}\left( [n]_{\times}^T \cdot [n]_{\times} \right)\\ &= 2\theta^2 \end{aligned}\]也就是说 $X$ 到 $Y$ 的测地距离为 $\sqrt{2}\theta$,这里的$\theta$ 是矩阵$X^TY$的旋转角。
3. 流形优化算法
3.1. 黎曼最速下降法
黎曼最速下降法以 $x_k$ 处的负黎曼梯度方向为搜索方向 \(\eta _k=-\mathrm{grad}f\left( x_k \right)\),然后通过线搜索寻找合适的步长 $t_k$,最后通过指数映射将切向量 $t_k\eta_k$ 映射到流形 $\mathcal{M}$ 上,作为下一个迭代点 $x_{k+1}= \mathrm{Exp}_{x_k}(t_k\eta_k)$。


3.2. 黎曼牛顿法
黎曼流形上的牛顿迭代步如下: \(x_{k+1}=x_{k}-\left(\operatorname{Hess} f\left(x_{k}\right)\right)^{-1}\left[\operatorname{grad} f\left(x_{k}\right)\right]\)
3.3. 原问题求解
由于原问题中的 Hess 阵恒为0,因此不能直接使用牛顿法,这里我们采用拟牛顿法进行求解。此外为了加快算法的收敛性,我们用 Huber 函数近似代替绝对值函数。该程序可通过调用 Manopt 优化库 实现。
4. 附录
4.1. 测地线的计算
计算 $\mathrm{SO}(3)$ 流形上以$X$ 为起点,沿切向量$H$ 方向延伸的测地线方程。
\[\gamma^T(t)\cdot \gamma(t)=I\] \[\dot{\gamma}^T(t)\cdot \gamma(t) + \gamma^T(t)\cdot \dot{\gamma}(t)=0\]设 $\Omega(t)=\gamma^T(t)\cdot \dot{\gamma}(t)$ ,显然 $\Omega(t)$ 是反对称矩阵,也有:
\[\dot{\gamma}(t)=\gamma(t)\cdot \Omega(t)\]$\dot{\gamma}(t)$ 显然是属于切平面 $T_{X}\mathrm{SO}(3)$的,因此沿曲线导数就是它本身:
\[\gamma '(t)= \mathcal{P} _{T_{\gamma \left( t \right)}\mathcal{M}}\left( \dot{\gamma}\left( t \right) \right)=\dot{\gamma}(t)\]于是可以计算:
\[\begin{aligned} \gamma ''(t)&= \mathcal{P} _{T_{\gamma \left( t \right)}\mathcal{M}}\left(\frac{\mathrm{d}}{\mathrm{d}t}\gamma '(t) \right)\\ &=\mathcal{P} _{T_{\gamma \left( t \right)}\mathcal{M}}\left( \ddot{\gamma}\left( t \right) \right)\\ &=\mathcal{P} _{T_{\gamma \left( t \right)}\mathcal{M}}\left( \dot{\gamma}(t)\cdot \Omega(t) + \gamma(t)\cdot \dot{\Omega}(t) \right)\\ \end{aligned}\]上文提到过投影的计算公式为:
\[\mathcal{P}_{T_X\mathrm{SO}(3)}\left( M \right)=X\mathrm{skew}\left( X^TM \right)\]可计算得:
\[\begin{aligned} &\gamma^T(t)\left( \dot{\gamma}(t)\cdot \Omega(t) + \gamma(t)\cdot \dot{\Omega}(t) \right)\\ &=\gamma^T(t)\cdot \dot{\gamma}(t)\cdot \Omega(t)+\gamma^T(t)\cdot {\gamma}(t)\cdot \dot{\Omega}(t)\\ &=\Omega^2(t)+\dot{\Omega}(t) \end{aligned}\]由于 $\Omega^2(t)$ 为对称阵,$\dot{\Omega}(t)$ 为反对称阵,因此有:
\[\gamma ''(t)=\gamma(t)\mathrm{skew}\left( \Omega^2(t)+\dot{\Omega}(t) \right)=\gamma(t) \cdot \dot{\Omega}(t)\] \[\dot{\Omega}(t)=\gamma^T(t) \gamma ''(t)\]由于 $\gamma(t)$ 为测地线,有$\gamma ‘‘(t)=0$ ,于是可推导出:
\[{\Omega}(t)=\gamma^T(0)\cdot \dot{\gamma}(0)=X^TH\]解微分方程 $\gamma(t)\cdot \Omega=\dot{\gamma}(t)$ 得:
\[\gamma \left( t \right) =X\exp \left( tX^TH \right)\]5. 相关书籍推荐
@hu_brief_2019 是袁亚湘团队对流形优化的一个简要介绍,可以看一看作为入门。
@boumal_introduction_2020 最近新出的一本介绍流形优化的书,排版精美内容详实,如果想深入了解的话强烈推荐看这本书。
@absil_optimization_2008 为数不多介绍矩阵流形的书,也可以看一看。
@boumal_discrete_2011 主要是 SO(3) 上的流形优化。
@sola_micro_2020 这个从机器人应用角度来介绍 SO(3) 上的李群理论。
@boumal_manopt_2013 是一个 MATLAB 的流形优化库,可以快速上手。
6. 参考文献
[1] J. Hu, X. Liu, Z. Wen, and Y. Yuan, “A Brief Introduction to Manifold Optimization,” arXiv:1906.05450 [math], Jun. 2019.
[2] N. Boumal, “An introduction to optimization on smooth manifolds,” Available online, Aug, 2020.
[3] P.-A. Absil, R. Mahony, and R. Sepulchre, Optimization algorithms on matrix manifolds. Princeton, N.J. ; Woodstock: Princeton University Press, 2008.
[4] N. Boumal and P.-A. Absil, “A discrete regression method on manifolds and its application to data on SO(n),” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 2284–2289, Jan. 2011, doi: 10.3182/20110828-6-IT-1002.00542.
[5] J. Solà, J. Deray, and D. Atchuthan, “A micro Lie theory for state estimation in robotics,” arXiv:1812.01537 [cs], Nov. 2020.
[6] N. Boumal, B. Mishra, P.-A. Absil, and R. Sepulchre, “Manopt, a Matlab toolbox for optimization on manifolds,” arXiv:1308.5200 [cs, math, stat], Aug. 2013.