本文主要解释了图结构上的 Laplace 算子，并且由此引申出图上的傅里叶基和傅里叶变换。 我们在频域上定义滤波函数对傅里叶系数进行修改，便得到了一种图滤波， 从空域角度来看，这就是图卷积。

1. 基础定义

1.1. 图与图信号

定义 (图)：对于加权无向图 $\mathcal{G} =(\mathcal{V} ,\mathcal{E} )$，其顶点集为 $ \mathcal{V}={1,\dots,n} $，边为$ \mathcal{E} \subset \mathcal{V}\times\mathcal{V}$ ，其权重 $ w_{ij}\geq 0 $ for $ (i,j)\in \mathcal{E} $​。

20210828132515094

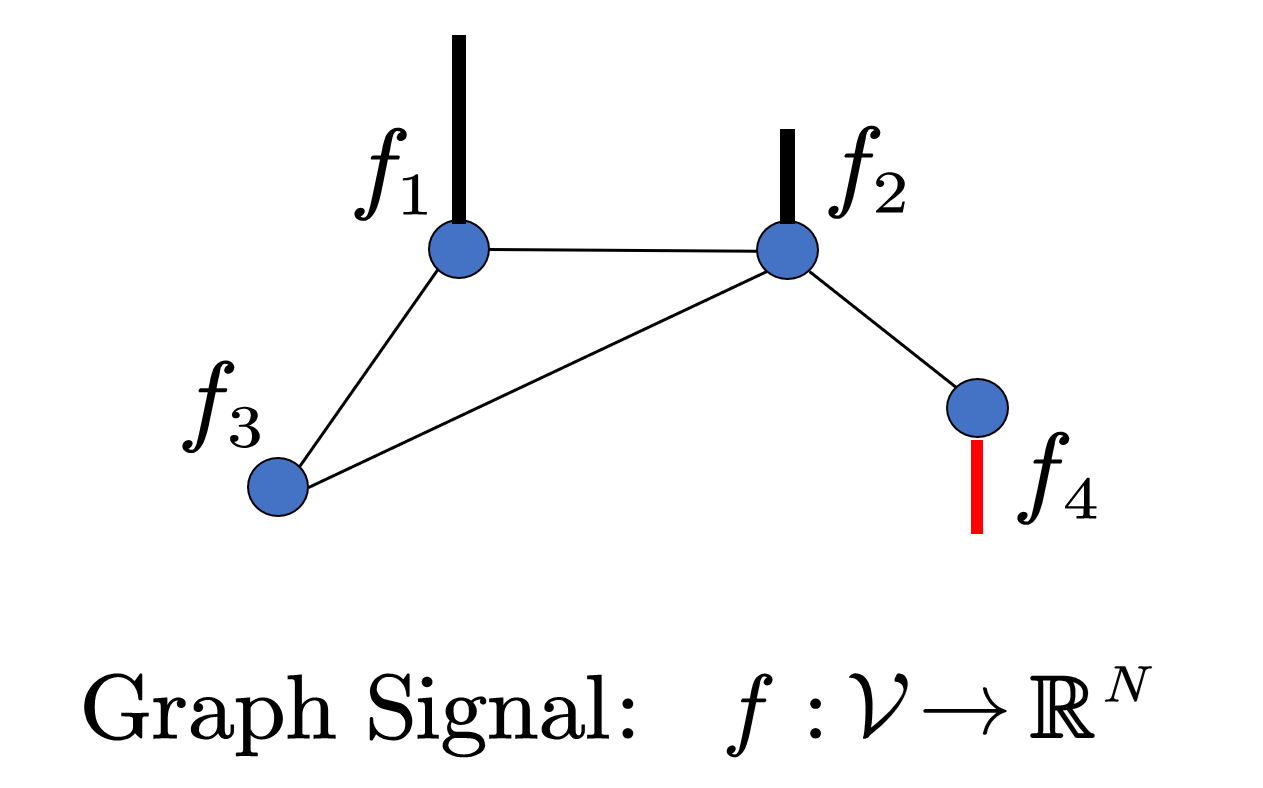
定义 (图信号)：图信号可以看作顶点上的函数 $ f\in L^{2}(\mathcal{V}) $​ ，每个顶点 $ i $​ 对应一个 $ f_i =f(i) $​ ，整体可表示成向量 $ \mathbf{f}=(f_1,\ldots,f_n) $​​。

20210828132554102

1.2. Laplace 矩阵

定义 (图 Laplace 算子)：图信号 $f$ 上的Laplace 算子定义为：

\[(\Delta f)_i=\sum_j{w_{ij} }\left( f_i-f_j \right)\]

为什么要这样定义呢，可以参看 附录：图 Laplace 算子的解释。

定义 (图 Laplace 矩阵)： $\Delta$ 算子可以用一个半正定矩阵 $\mathbf{L}$​ 来代替：

\[\mathbf{L} =\mathbf{D}-\mathbf{W}\]

其中 $ \mathbf{W} $ 是加权邻接矩阵， $ \mathbf{D}=\mathrm{diag}\left( \sum_{j}{w_{ij} } \right) $ 是对角阵（相当于把$ \mathbf{W}$的每一行加到对角元上）。

\[{\color[RGB]{240, 0, 0} \mathbf{L} }\mathbf{f}={\color[RGB]{240, 0, 0} \left( \mathbf{D}-\mathbf{W} \right) }\mathbf{f}=\left[ \begin{array}{c} \vdots\\ \sum_j{w_{ij}\left( f_i-f_j \right)}\\ \vdots\\ \end{array} \right]\]

$\mathbf{L}$ 是实对称矩阵， 其特征分解形式如下：

\[\begin{aligned} \mathbf{L}&=\mathbf{U\Lambda U}^{\top}=\left[ \begin{matrix} \mathbf{u}_1& \mathbf{u}_2& \cdots& \mathbf{u}_n\\ \end{matrix} \right] \left[ \begin{matrix} \lambda _1& & & \\ & \lambda _2& & \\ & & \ddots& \\ & & & \lambda _n\\ \end{matrix} \right] \left[ \begin{array}{c} \mathbf{u}_{1}^{\top}\\ \mathbf{u}_{2}^{\top}\\ \vdots\\ \mathbf{u}_{n}^{\top}\\ \end{array} \right]\\ &=\sum_{i=1}^n{\lambda _i}\mathbf{u}_i\mathbf{u}_{i}^{\top}\\ \end{aligned}\]

其中 \(\mathbf{L}\mathbf{u}_i=\lambda_{i}\mathbf{u}_i\)， 并且特征值 $\lambda_{i}\geq 0$。

此外，图 Laplace 矩阵 $\mathbf{L}$ 有下列性质，证明见 附录：图 Laplace 算子的性质。

  1. 最小特征值为0。
  2. 零特征值对应的特征向量在同一连通分支上的值都相等。
  3. 连通图中， $\mathbf{L}$ 零特征值重数为1。
  4. 零特征值的重数，等于图中连通分支的个数。

1.3. 图信号的总变差

定义 (图信号的总变差)：也可以看作图上的Dirichlet 能量，衡量了图信号的光滑程度。

\[\left\| f \right\| _{\mathrm{Dir} }^{2}=\frac{1}{2}\sum_{i,j}{w_{ij} }\left( f_i-f_j \right) ^2=\mathbf{f}^{\top}\mathbf{Lf}\]

在连续流形上，Dirichlet 能量的定义为：

\[\left\| f \right\| _{\mathrm{Dir} }^{2}=\langle \nabla f,\nabla f\rangle =\langle f,\Delta f\rangle =\int{f\left( x \right) \Delta f\left( x \right) \,\mathrm{d}x}\]

2. 图傅里叶变换

2.1. 传统傅里叶变换

给定一组单位正交基 \(\left\{ \phi _k\left( x \right) \right\}_{k=1}^{+\infty}\)，我们可以将函数 $f(x)$ 投影到这组正交基上：

\[f\left( x \right) =\sum_{k=1}^{+\infty}{\underset{ {\color[RGB]{240, 0, 0} \hat{f}_k} }{\underbrace{\left< f,\phi _k \right> } }}\phi _k\]

我们将 $\langle f,\phi _k\rangle $ 记为 $\hat{f}_k$，这表示在基 $\phi _k$ 上的系数，也可以看作关于 $k$ 的一个函数：

\[\hat{f}\left( k \right) =\langle f,\phi _k\rangle =\frac{1}{2L}\int_{-L\,\,}^L{f\left( x \right) \overline{\phi _k\left( x \right) }\,\mathrm{d}x\,}\]

同时，$f$ 本身也可表示成 $\hat{f}$​ 和 $\phi$ 的内积：

\[f\left( x \right) =\langle \hat{f},\phi \rangle =\sum_k{\hat{f}_k\phi _k\left( x \right)}\]

如果，我们把傅里叶基 \(\left\{ 1,\mathrm{e}^{\mathrm{i}x},\mathrm{e}^{\mathrm{i}2x},... \right\}\) 带入到这个基函数中：

\[\begin{aligned} f\left( x \right) &=\sum_{k=0}^{+\infty}{\langle f,\mathrm{e}^{\mathrm{i}kx} \rangle}\mathrm{e}^{\mathrm{i}kx} \\ &=\sum_{k=0}^{+\infty}{\frac{1}{2\pi}\int_{-\pi \,\,}^{\pi}{f\left( \omega \right) \mathrm{e}^{-\mathrm{i}k\omega}\,\mathrm{d}\omega }\cdot}\mathrm{e}^{\mathrm{i}kx} \\ &=\sum_{k=0}^{+\infty}\hat{f}_k\mathrm{e}^{\mathrm{i}kx} \\ &=\langle \hat{f}_k ,\mathrm{e}^{\mathrm{i}kx} \rangle \end{aligned}\]

其实这就是傅里叶变换：

\[\begin{matrix} \hat{f}(k)=\langle f,\mathrm{e}^{\mathrm{i}kx}\rangle =\frac{1}{2\pi}\int_{-\pi \,\,}^{\pi}{f\left( \omega \right) \mathrm{e}^{-\mathrm{i}k\omega}\,\mathrm{d}\omega}& {\color[RGB]{0, 0, 240} \text{傅里叶变换} }\\ f\left( x \right) =\langle \hat{f},\mathrm{e}^{\mathrm{i}kx}\rangle =\sum_{k=0}^{+\infty}{\hat{f}(k)}\mathrm{e}^{\mathrm{i}kx}& {\color[RGB]{0, 0, 240} \text{傅里叶逆变换} }\\ \end{matrix}\]

2.2. 图傅里叶变换

傅里叶基是 Laplace 算子的特征函数：

\[\Delta \mathrm{e}^{-\mathrm{i}kx}=-k^2\mathrm{e}^{-\mathrm{i}kx}\]

而 Laplace 矩阵的特征向量也刚好构成了一组单位正交基，于是我们可以认为它就是图上的傅里叶基。

\[\mathbf{Lu}_k=\lambda _k\mathbf{u}_k\]

我们将 $\mathbf{f}\in \mathbb{R}^n$ 投影到这组正交基上：

\[\mathbf{\hat{f} }_k=\left. \langle \mathbf{f},\mathbf{u}_k \right. \rangle =\mathbf{f}^{\top}\mathbf{u}_k\]

写成矩阵形式就是 $\mathbf{\hat{f} }=\mathbf{U}^{\top}\mathbf{f}$，那么如何用系数 $\mathbf{\hat{f} }_k$ 来表示 $\mathbf{f}$ 呢？由于 $\mathbf{U}$​ 是正交阵，所以有：

\[\mathbf{f}=\mathbf{UU}^{\top}\mathbf{f}=\mathbf{U\hat{f} }\]

总结起来，图上的傅里叶变换为：

\[\begin{matrix} \mathbf{\hat{f} }=\mathbf{U}^T\mathbf{f}& {\color[RGB]{0, 0, 240} \text{傅里叶变换} }\\ \mathbf{f}=\mathbf{U\hat{f} }& {\color[RGB]{0, 0, 240} \text{傅里叶逆变换} }\\ \end{matrix}\]

2.3. 傅里叶基的频率

傅里叶基的频率（也就是变化快慢）与特征值的大小密切相关。以欧式空间中的傅里叶基 \(\left\{ 1,\mathrm{e}^{\mathrm{i}x},\mathrm{e}^{\mathrm{i}2x},... \right\}\) 为例，其特征值 $-k^2$ 的绝对值越小，$\mathrm{e}^{\mathrm{i}kx}=\cos kx+\mathrm{i}\sin kx$ 的变化越缓慢。

sin

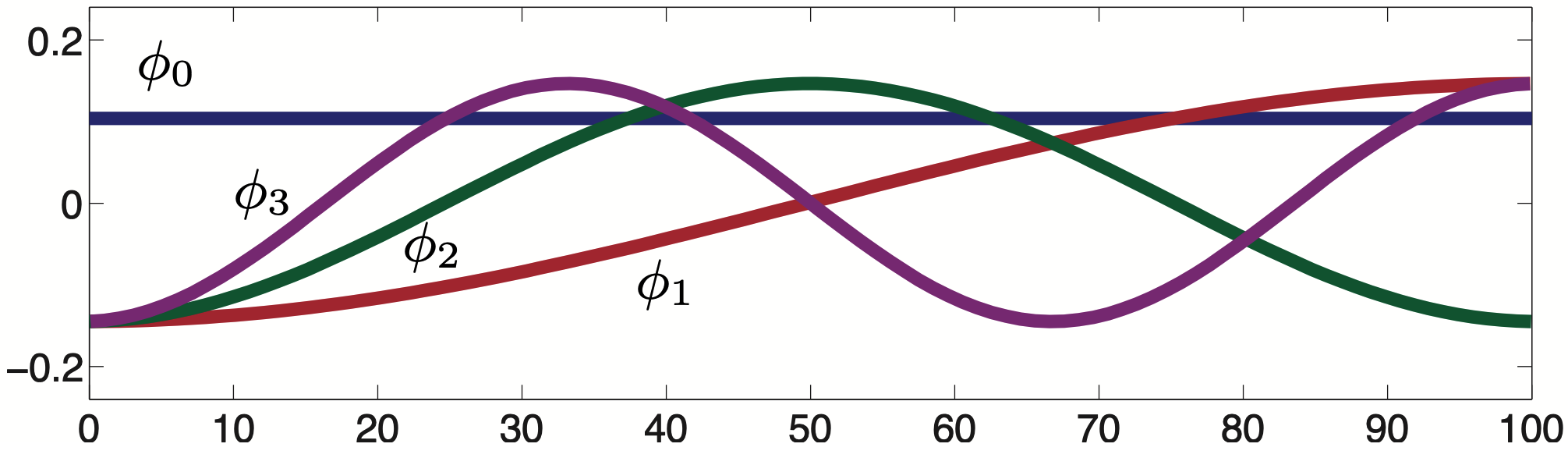
在图上也有类似的性质：因为 $\mathbf{u}_k$ 的总变差就等于 $\lambda_k$​，所以 $\lambda _k$​​ 越小，$\mathbf{u}_k$ 在顶点上的变化越小。

\[\left\| \mathbf{u}_k \right\| _{\mathrm{Dir} }^{2}=\mathbf{u}_k^{\top}\mathrm{L}\mathbf{u}_k=\mathbf{u}_k^{\top}\lambda _k\mathbf{u}_k=\lambda _k\]

graph

当 $\lambda _l=0$ 时，$\mathbf{u}_l$ 在同一连通分支上的值就都相等了（对应上图中的 $\phi_1$）。

3. 图滤波

所谓滤波就是过滤掉特定频率的信息，来达到想要的效果。

3.1. 图像上的滤波

以下图为例，左边是鸭子，右边是傅里叶变换得到的频率图，频率图越靠近中心，代表的频率越小。如果我们只保留中心一圈的频率信息，也就是只让低频信息通过，这就得到了一个低通滤波，逆变换得到的图像看起来更平滑，高通滤波则恰好相反。

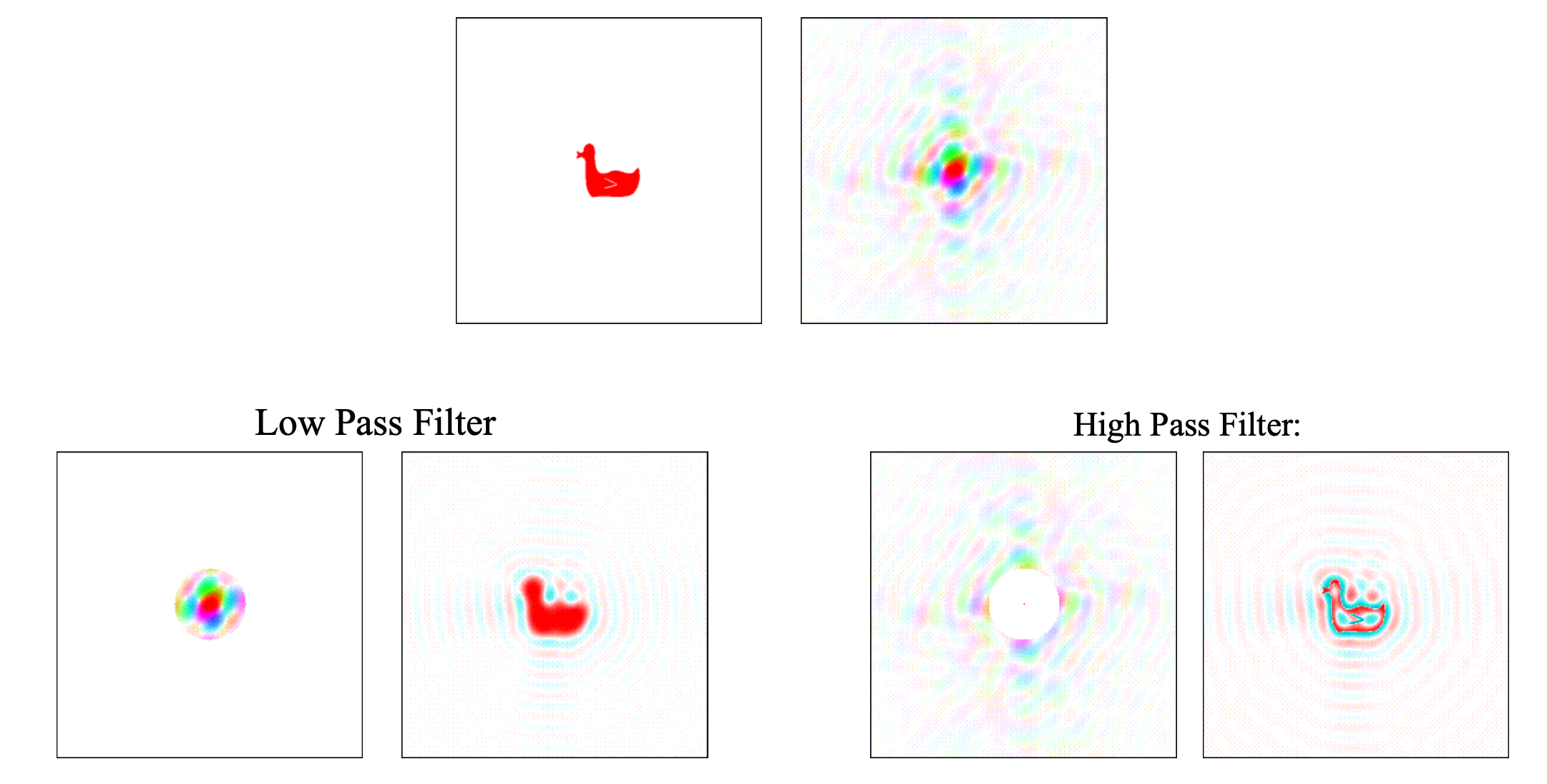
image-20210828212204966

此外，由于频域上的点积等价于在空间上的卷积，因此卷积也可以看做是一种滤波。

\[\begin{aligned} f\star g &=\sum_k{\langle f,\phi _k \rangle \langle g,\phi _k \rangle \phi _k} \\ &=\sum_k \hat{f}\cdot\hat{g}\phi _k \end{aligned}\]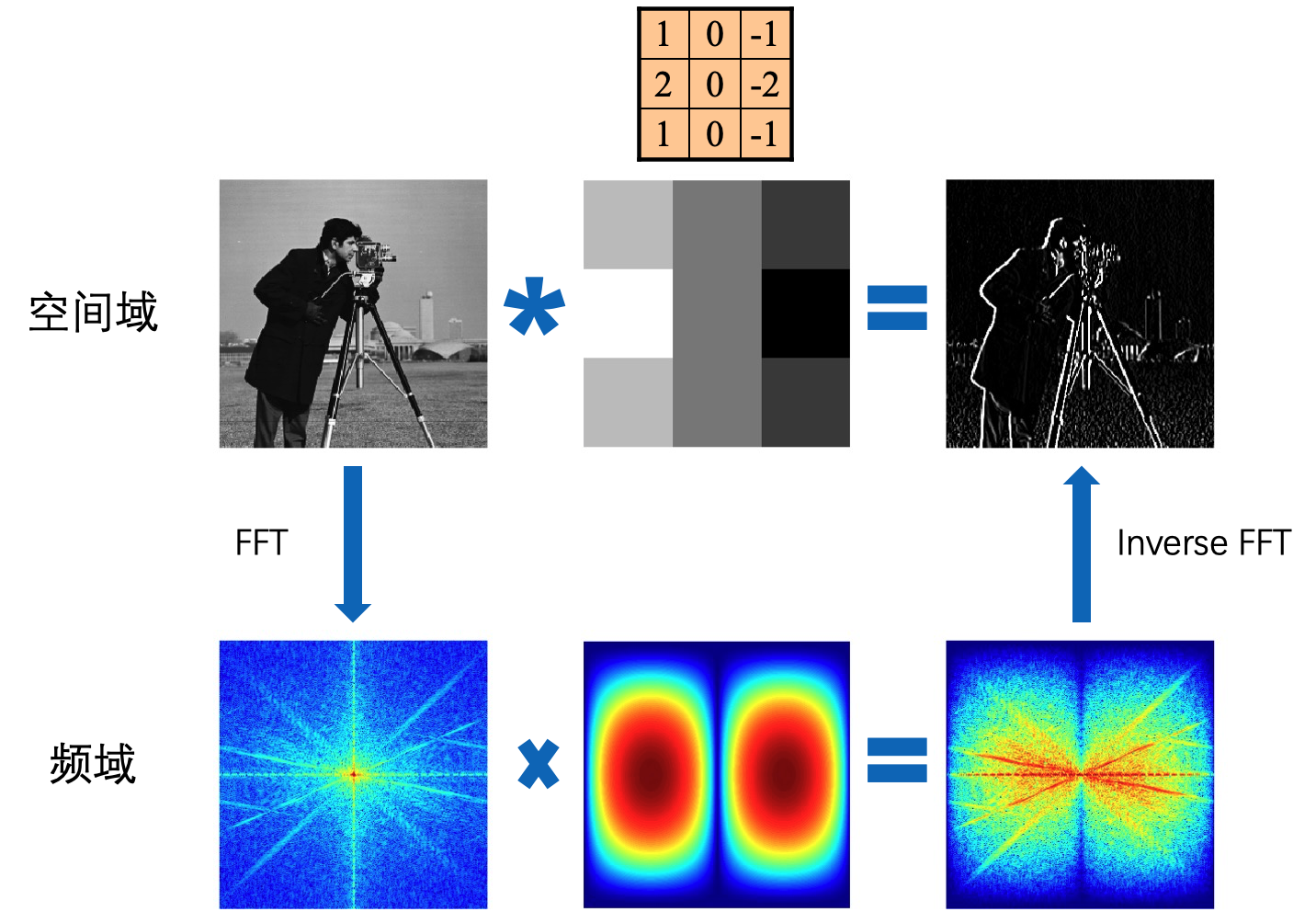

image-20210828212438065

3.2. 图滤波

对于输入的图信号 \(\mathbf{f}_{\mathrm{in} }\)，我们将其与函数 $\mathbf{g}$ 做卷积，得到输出信号 $\mathbf{f}_{\mathrm{out} }$。

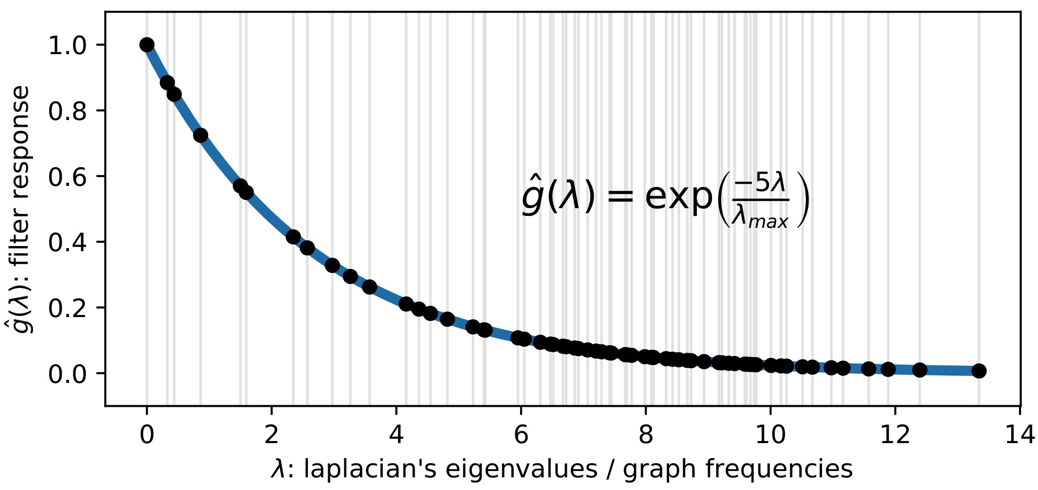
\[\begin{aligned} \mathbf{f}_{\mathrm{out} }&=\mathbf{f}_{\mathrm{in} }\star \mathbf{g}\\ &={\color[RGB]{240, 0, 0} \mathcal{F} ^{-1} }\left[ \mathbf{\hat{f} }_{\mathrm{in} }\odot {\color[RGB]{0, 0, 240} \mathbf{\hat{g} }} \right]\\ &={\color[RGB]{240, 0, 0} \mathbf{U} }{\color[RGB]{0, 0, 240} \left[ \begin{matrix} \hat{g}\left( \lambda _1 \right)& & 0\\ & \ddots& \\ 0& & \hat{g}\left( \lambda _n \right)\\ \end{matrix} \right] }\mathbf{U}^{\mathrm{T} }\mathbf{f}_{\mathrm{in} }\\ \end{aligned}\]

$\mathbf{\hat{f} }_{\mathrm{in} }$ 是不同频率基的系数，因此我们可以通过点乘 $\hat{g}\left( \lambda_k \right)$ 来修改 $\lambda _k$​ 频率的系数，一个常见的滤波就是热核函数。

image-20210828213246301

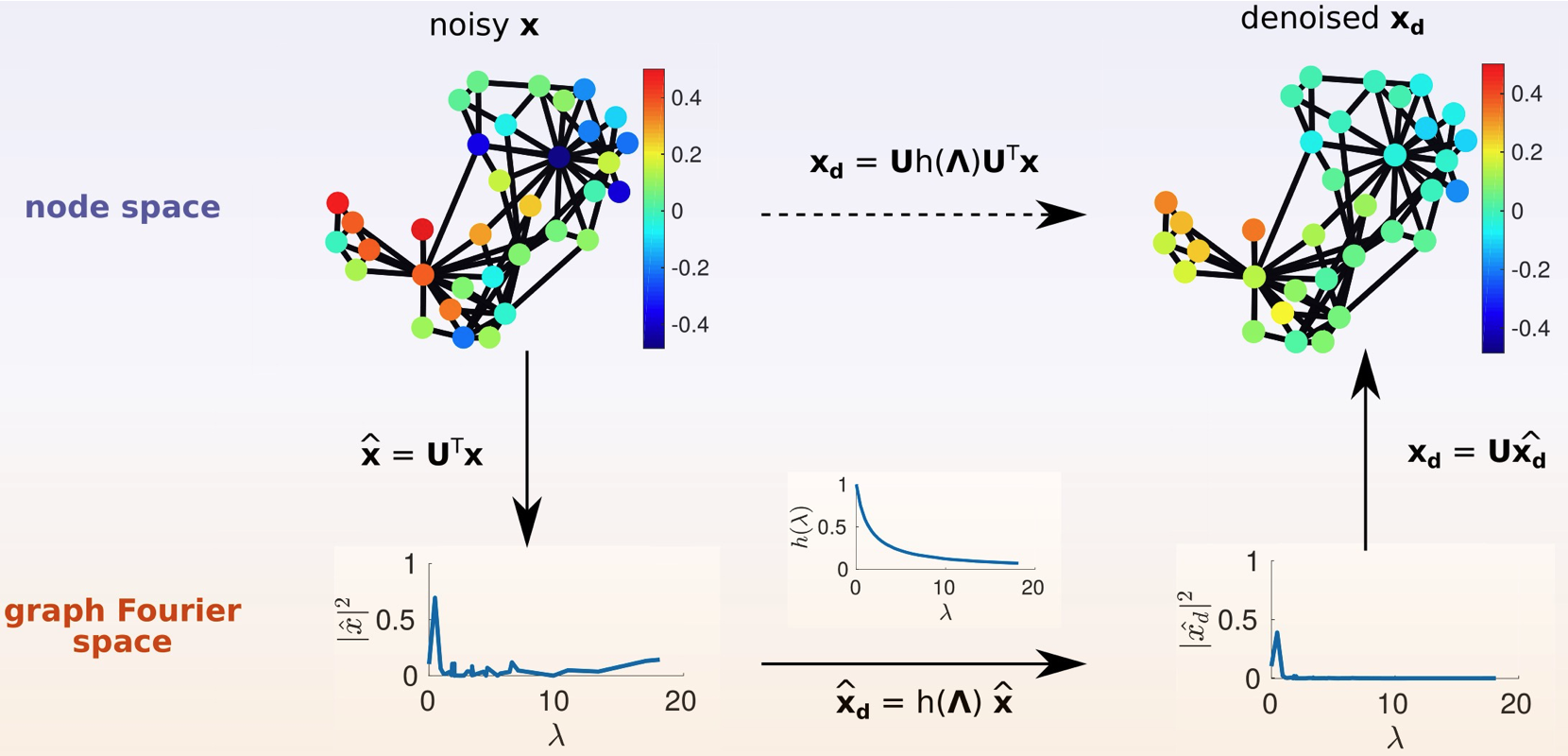
对图信号降噪的流程大致如下：

image-20210828213331499

3.3. 空间局部性

在图像卷积中，每个输出像素都仅由周围像素参与卷积运算得到，邻域的范围就是卷积核的尺寸。那如何让图卷积也具有空间上的局部性呢？

如果滤波函数 $\hat{h}(\lambda_l)$​​ 为 K 阶多项式：

\[\hat{h}\left( \lambda _l \right)=\sum_{k=0}^K{a_k\lambda _{l}^{k} }\]

那么有：

\[\begin{aligned} \mathbf{f}_{\mathrm{out} }&=\mathbf{U}\left[ \begin{matrix} \widehat{h}\left( \lambda _1 \right)& & 0\\ & \ddots& \\ 0& & \widehat{h}\left( \lambda _n \right)\\ \end{matrix} \right] \mathbf{U}^{\mathrm{T} }\mathbf{f}_{\mathrm{in} }\\ &=\sum_{k=1}^K{a_k\mathbf{U}\left[ \begin{matrix} \lambda _{1}^{k}& & 0\\ & \ddots& \\ 0& & \lambda _{n}^{k}\\ \end{matrix} \right] \mathbf{U}^{\mathrm{T} }}\mathbf{f}_{\mathrm{in} }\\ &=\sum_{k=0}^K{a_k\mathbf{L}^k}\mathbf{f}_{\mathrm{in} }\\ \end{aligned}\]

注意到 $L^k$ 代表了 k 次可达性：如果 $j$ 不在 $i$ 的 k-hop 邻域内，那么就有 $\left( \mathbf{L}^k \right) _{ij}=0$，证明见 附录：L^k 的 k 次可达性。

也就是说 $\mathbf{f}_{\mathrm{out} }(i)$​ 只受其 K-hop 邻域 $\mathcal{N}_K\left( i \right) $​​ 内顶点的影响，这就具有了空间上的局部性。

4. 对比总结

  欧式空间 图傅里叶
特征方程 $\Delta \mathrm{e}^{-\mathrm{i}kx}=-k^2\mathrm{e}^{-\mathrm{i}kx}$ $\mathbf{Lu}_k=\lambda_k\mathbf{u}_k$
傅里叶基 $\mathrm{e}^{-\mathrm{i}kx}$ $\mathbf{u}_k$
傅里叶变换 $\hat{f}_k=\langle f ,\mathrm{e}^{\mathrm{i}kx} \rangle$ $\mathbf{\hat{f}}=\mathbf{U}^{\top}\mathbf{f}$
傅里叶逆变换 $f=\langle \hat{f} ,\mathrm{e}^{\mathrm{i}kx} \rangle$ $\mathbf{f}=\mathbf{U\hat{f}}$
卷积公式 $f\star g=\langle \hat{f}\cdot \hat{g},\mathrm{e}^{\mathrm{i}kx}\rangle $ $\mathbf{f}\star \mathbf{g}=\mathbf{U}\left( \mathbf{\hat{f}}\odot \mathbf{\hat{g}} \right) $

5. 附录

5.1. 图 Laplace 算子的解释

图 Laplace 算子为什么会定义成 \((\Delta f)_i=\sum_j{w_{ij} }\left( f_i-f_j \right)\) 这种形式呢？

首先，Laplace 算子的定义为梯度的散度，即：

\[\Delta f=\nabla \cdot \left( \nabla f \right) =\mathrm{div}\left( \nabla f \right)\]

在 $\mathbb{R}^n$​​​ 中，Laplace 算子是一个二阶微分算子，即在各个维度求二阶导数后求和：

\[\Delta f=\sum_i{\frac{\partial ^2f}{\partial x_{i}^{2} }}\]

在一维离散情况下，有

\[\frac{\partial f}{\partial x}=f^{\prime}\left( x \right) =f\left( x+1 \right) -f\left( x \right)\] \[\frac{\partial ^2f}{\partial x^2}=f^{\prime\prime}\left( x \right) =f^{\prime}\left( x+1 \right) -f^{\prime}\left( x \right) =f\left( x+1 \right) +f\left( x-1 \right) -2f\left( x \right)\]

在二维离散情况下（例如图像处理中），有

\[\Delta f=\frac{\partial ^2f}{\partial x^2}+\frac{\partial ^2f}{\partial y^2}=f\left( x+1,y \right) +f\left( x-1,y \right) +f\left( x,y+1 \right) +f\left( x,y-1 \right) -4f\left( x,y \right)\]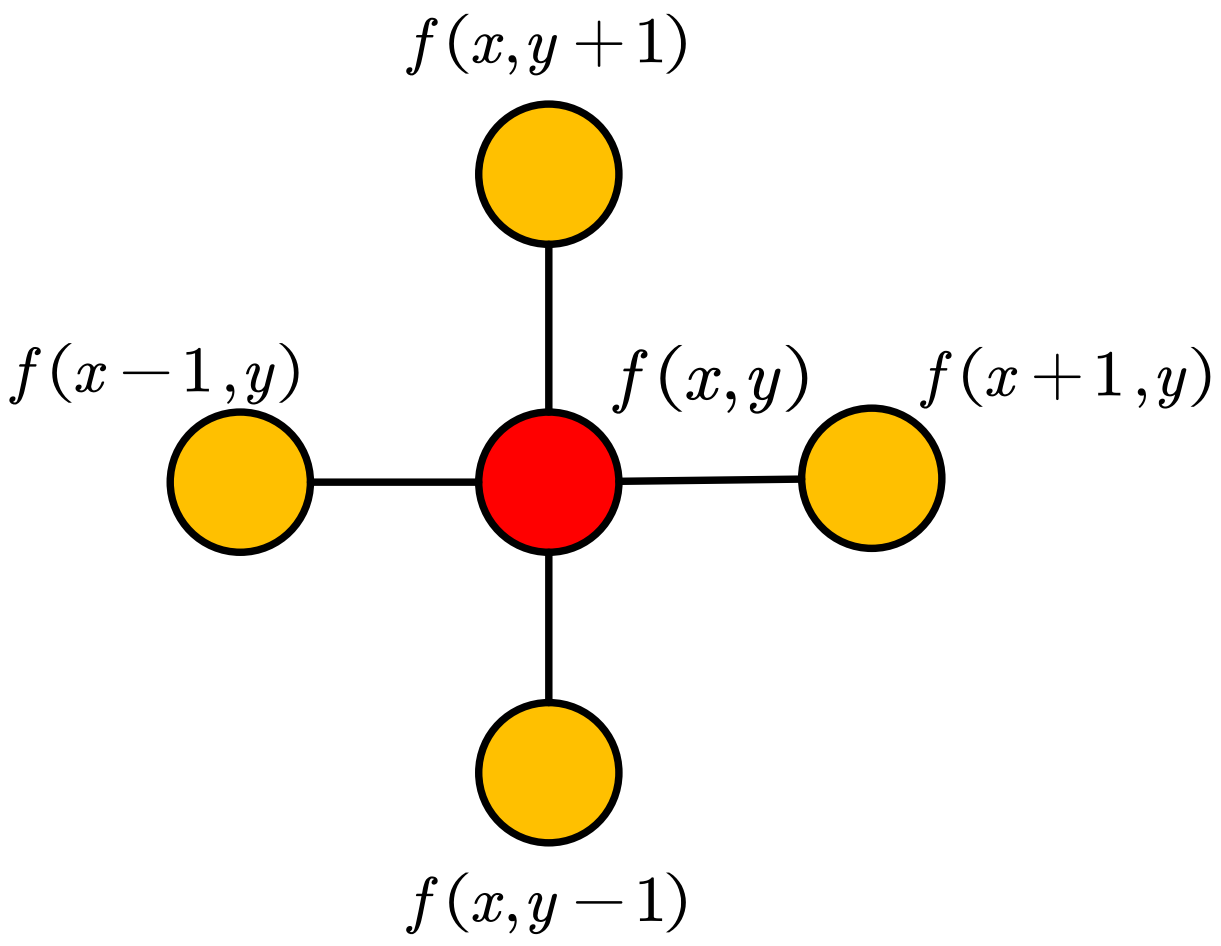

20210828134930247

在三角网格上， Laplace-Beltrami 定义为：

\[\Delta f\left( v_i \right) =\frac{1}{a_i}\sum_{v_j\in \mathcal{N} \left( v_i \right)}{\frac{1}{2}\left( \cot \alpha _{i,j}+\cot \beta _{i,j} \right)}\left( f_j-f_i \right)\]

其中 $a_i$ 是中间红色区域的面积。

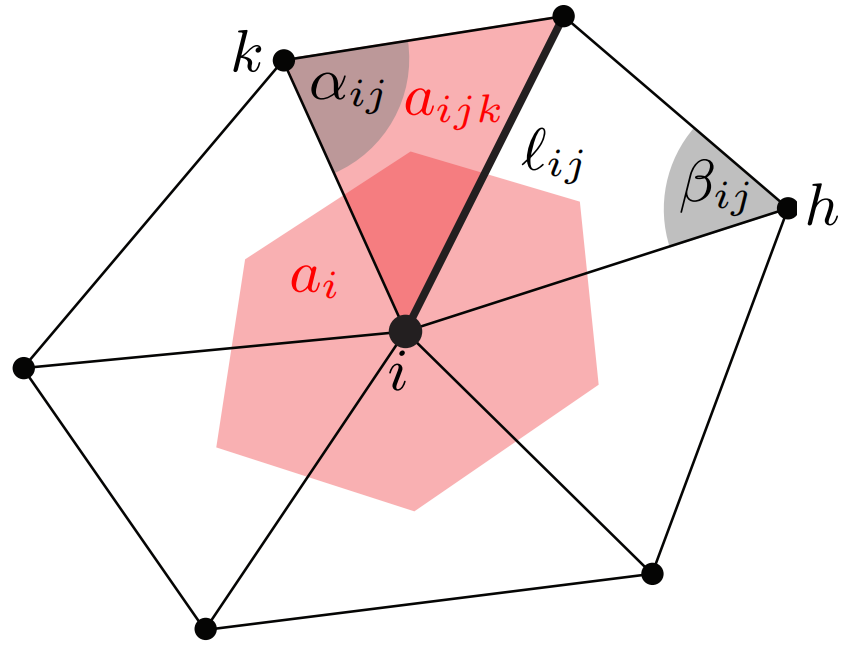
20210828141816568

可以看到，这个定义和图非常相似，就是把权重定义设成了 $w_{ij}=\frac{1}{2}\left( \cot \alpha_{i,j}+\cot \beta _{i,j} \right) $​。

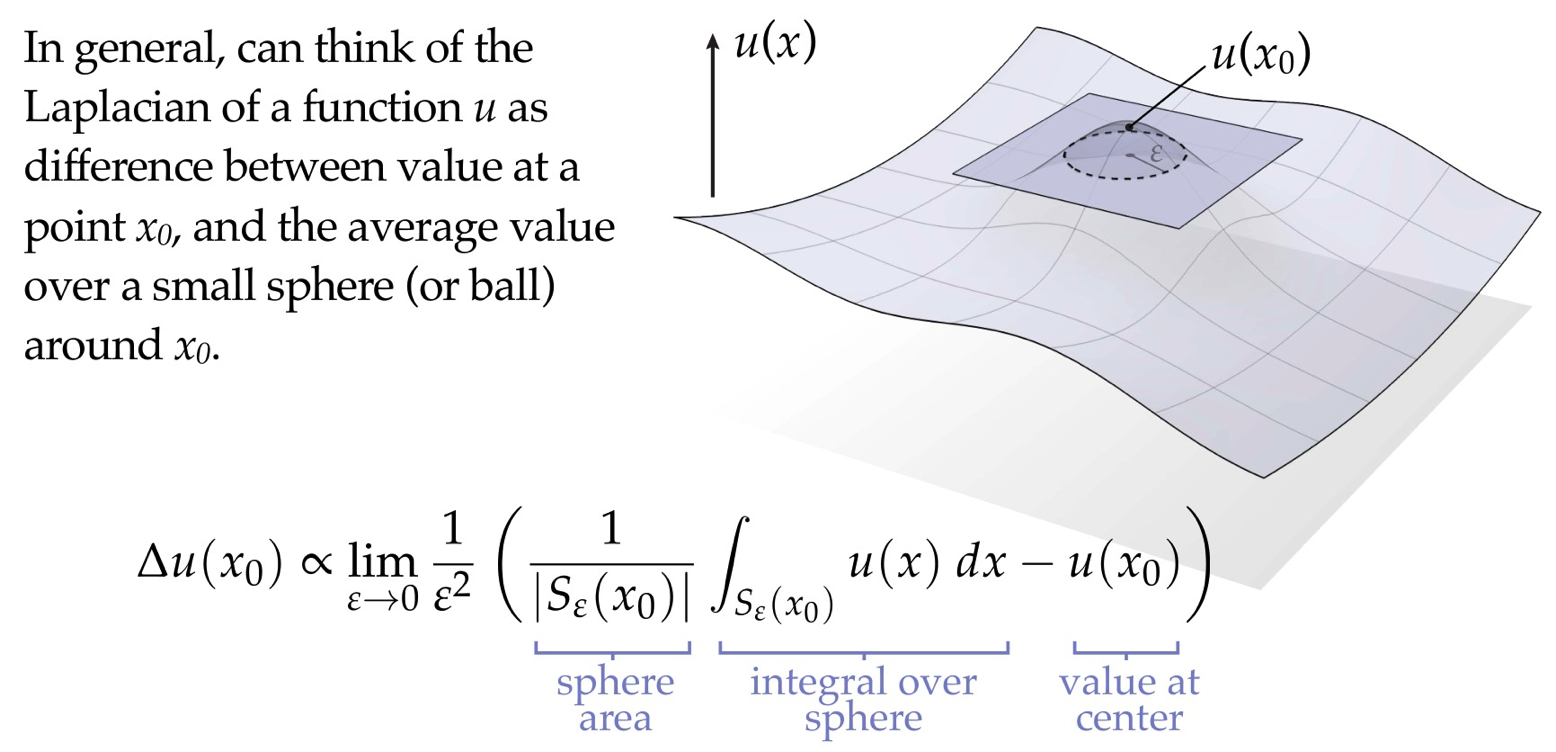
image-20210828211723577

总结起来的话，就是 Laplace 算子描述了当前点与其邻域平均值之间的差异。

此外，论文《Geometric deep learning: going beyond Euclidean data》从数学的角度较为严谨地对图 Laplace 算子进行了定义：对于图 $\mathcal{G}=(\mathcal{V}, \mathcal{E})$，$a_i$ 为顶点 $i$ 上的权重，$w_{i j} \geq 0$ 为边 $(i, j) \in \mathcal{E}$ 上的权重。 $f: \mathcal{V} \rightarrow \mathbb{R}$ 是作用在顶点上的函数，$F: \mathcal{E} \rightarrow \mathbb{R}$ 是定义在边上的函数并且有 $F_{ij}=-F_{ji}$ ，分别定义顶点和边上的内积：

\[\langle f,g\rangle _{L^2(\mathcal{V} )}=\sum_{i\in \mathcal{V}}{a_i}f_ig_i\] \[\langle F,G\rangle _{L^2(\mathcal{E} )}=\sum_{\left( i,j \right) \in \mathcal{E}}{w_{ij}}F_{ij}G_{ij}\]

图上的梯度算子 $\nabla: L^{2}(\mathcal{V}) \rightarrow L^{2}(\mathcal{E})$ 定义为：

\[(\nabla f)_{ij}=f_i-f_j\]

图上的散度算子定义 $\mathrm{div}: L^{2}(\mathcal{E}) \rightarrow L^{2}(\mathcal{V})$ 定义为：

\[(\mathrm{div}F)_i=\frac{1}{a_i}\sum_{j:(i,j)\in \mathcal{E}}{w_{ij}}F_{ij}\]

可以验证梯度算子 $\nabla$​ 和散度算子 $\mathrm{div}$ 为伴随算子：

\[\langle F,\nabla f\rangle _{L^2(\mathcal{E} )}=\langle \mathrm{div}F,f\rangle _{L^2(\mathcal{V} )}\]

Proof：

\[\langle F,\nabla f\rangle _{L^2(\mathcal{E} )}=\sum_{\left( i,j \right) \in \mathcal{E}}{w_{ij}F_{ij}\left( \nabla f \right) _{ij}}=\sum_{\left( i,j \right) \in \mathcal{E}}{w_{ij}F_{ij}\left( f_i-f_j \right)}\] \[\begin{aligned} \langle \mathrm{div}F,f\rangle _{L^2(\mathcal{V} )}&=\sum_{i\in \mathcal{V}}{\sum_{j:(i,j)\in \mathcal{E}}{w_{ij}F_{ij}f_i}}\\ &=\sum_{\left( i,j \right) \in \mathcal{E}}{w_{ij}F_{ij}f_i}+\sum_{\left( j,i \right) \in \mathcal{E}}{w_{ij}F_{ij}f_i}\\ &=\sum_{\left( i,j \right) \in \mathcal{E}}{w_{ij}F_{ij}\left( f_i-f_j \right)} \end{aligned}\]

然后可以通过 $\Delta=\operatorname{div} \nabla$ 推导出 Laplace 算子 $\Delta: L^{2}(\mathcal{V}) \rightarrow L^{2}(\mathcal{V})$ ：

\[\begin{aligned} (\Delta f)_i&=\left( \mathrm{div}\nabla f \right) _i\\ &=\frac{1}{a_i}\sum_{j:(i,j)\in \mathcal{E}}{w_{ij}}(\nabla f)_{ij}\\ &=\frac{1}{a_i}\sum_{j:(i,j)\in \mathcal{E}}{w_{ij}}\left( f_i-f_j \right)\\ \end{aligned}\]

5.2. 图 Laplace 算子的性质

最小特征值为0。

Proof：由于 $\mathbf{L}$ 的每一列加起来都为0，因此其行列式为0，也就至少有一个 0 特征值。

零特征值对应的特征向量在同一连通分支上的值都相等。

Proof：由 $\mathbf{Lu}_l=0$ 即可得

\[\mathbf{u}_l^{\top}\mathbf{L}\mathbf{u}_l=\frac{1}{2}\sum_{i,j}{w_{ij} }\left( \mathbf{u}_l\left( i \right) -\mathbf{u}_l\left( j \right) \right) ^2=0\]

如果 $i$ 和 $j$ 处在同一连通分支，那么 $w_{ij}>0$​，则必然有 $\mathbf{u}_l\left( i \right) =\mathbf{u}_l\left( j \right)$​ 。

连通图中， $\mathbf{L}$ 零特征值重数为1。

Proof：如果零特征值重数大于1的话，则至少有两个不相关的基 $\mathbf{u}_1$ 和 $\mathbf{u}_2$ 使得 $\mathbf{Lu}_1=\mathbf{Lu}_2=0$，但我们知道 $\mathbf{u}_1$ 在所有顶点上的值都相等，$\mathbf{u}_2$ 同理，因此 $\mathbf{u}_1$ 和 $\mathbf{u}_2$ 是线性相关的，与假设矛盾。

零特征值的重数，等于图中连通分支的个数。

Proof：假定图中连通分量的个数为 $k$ ，我们可以将同一连通分支的顶点放在一起，这样得到的邻接矩阵 $\mathbf{W}$ 会呈现对角块结构，相应的 $\mathbf{L}$ 也会有对角块结构：

\[\mathbf{L}=\left[ \begin{matrix} \mathbf{L}_1& & & \\ & \mathbf{L}_2& & \\ & & \ddots& \\ & & & \mathbf{L}_k\\ \end{matrix} \right]\]

其中每个块 $\mathbf{L}_i$​ 对应于第 $i$​ 个连通子图的 Laplace 矩阵，可知每个 $\mathbf{L}_i$​​ 中都会有一个零特征值，因此整个图的零特征值重数等于子块的个数。

从另一个角度来看，如果我们知道任意 $n-1$ 个顶点的连边信息，那么就能推出剩下那个顶点的连边信息，反映在邻接矩阵上 $\mathbf{W}$ ，就是 $\mathbf{W}$ 的任意一列都可以由其他 $n-1$ 列的线性组合表示，而度矩阵 $\mathbf{D}$ 也是 $\mathbf{W}$ 的线性组合，因此图中每多一个连通分支， $\mathbf{L}$ 中就会多一列冗余表示，也就多了一重零特征值。

5.3. L^k 的 k 次可达性

若顶点 $i$ 到顶点 $j$ 的距离大于 $K$，那么有 $\left( \mathbf{L}^K \right) _{ij}=0$。

Proof：首先定义二值邻接矩阵 $\mathbf{A}$，如果 $i$ 和 $j$ 相连则 \(\mathbf{A}_{ij}=1\)，否则为0，并且令对角元 \(\mathbf{A}_{ii}=1\)。

那么 $( \mathbf{A}^k )_{ij}$ 代表着从 $i$ 到$j$ 长度小于等于$k$ 的路径的数目：

\[\left( \mathbf{A}^k \right) _{ij}=\sum{\mathbf{A}_{is_1}\mathbf{A}_{s_1s_2}\cdots \mathbf{A}_{s_{n-1}j} }\] \[\left( \mathbf{L}^k \right) _{ij}=\sum{\mathbf{L}_{is_1}\mathbf{L}_{s_1s_2}\cdots \mathbf{L}_{s_{n-1}j} }\]

由于 $\mathbf{A}$ 是非负的，因此 \(\left( \mathbf{A}^k \right)_{ij}=0\) 说明了任意路径 \(\mathbf{A}_{is_1}\mathbf{A}_{s_1s_2}\cdots \mathbf{A}_{s_{n-1}j}\) 中都至少有一个 \(\mathbf{A}_{s_ms_n}=0\)，而 \(\mathbf{A}_{s_ms_n}=0\) 则必然有 \(\mathbf{L}_{s_ms_n}=0\)，因此 $\left( \mathbf{A}^k \right)_{ij}=0$ 可推出 $\left( \mathbf{L}^k \right) _{ij}=0$。

5.4. 归一化 Laplace 矩阵

最后介绍一些 Laplace 矩阵的归一化变体。

5.4.1. Symmetric normalized Laplacian

该变体是将权重 $\mathbf{W}_{ij}$ 乘上一个缩放因子 $\frac{1}{\sqrt{d_id_j} }$，其定义为：

\[\mathbf{L}_{\mathrm{sym} }=\mathbf{D}^{-\frac{1}{2} }\mathbf{LD}^{-\frac{1}{2} }=\mathbf{I}-\mathbf{D}^{-\frac{1}{2} }\mathbf{WD}^{-\frac{1}{2} }\]

对称归一化 Laplace 算子的特征值取值范围为 $[0,2]$，最大特征值 $\lambda_{\mathrm{max} }=2$ 时当且仅当 $\mathcal{G}$ 为一个二分图，证明可参考《图的拉普拉斯矩阵的特征值范围的一个估计》。

5.4.2. Random walk normalized Laplacian

另一种常用的 Laplace 矩阵为随机游走归一化 Laplace 矩阵：

\[\mathbf{P}=\mathbf{D}^{-1}\mathbf{W}\]

该矩阵中每个元素 $\mathbf{P}_{ij}$ 表示 Markov 随机漫步时从顶点 $i$ 一步走到 $j$ 的概率。

5.4.3. Asymmetric normalized Laplacian

非对称归一化 Laplace 矩阵定义为：

\[\mathbf{L}_{\mathrm{a} }= \mathbf{D}^{-1}\mathbf{L}= \mathbf{I}_{n}-\mathbf{D}^{-1}\mathbf{W}\]

注意到 \(\mathbf{L}_{\mathrm{a} }\) 跟 \(\mathbf{L}_{\mathrm{sym} }\) 有相同的特征值。如果 \(\mathbf{L}_{\mathrm{sym} }\) 有特征值 $\lambda_l$ 和对应的特征向量 $\mathbf{u}_l$，那么 \(\mathbf{L}_{\mathrm{a} }\) 也会有特征值 $\lambda_l$ 和特征向量 \(\mathbf{D}^{-\frac{1}{2} }\mathbf{u}_l\)。

5.5. 图像傅立叶变换代码

clc,clear,close all
im = double(imread('cameraman.tif'))/255; 
[imh, imw] = size(im);

fil =  fspecial('sobel')';

fftsize = 1024;  % should be order of 2 (for speed)
im_fft  = fft2(im,  fftsize, fftsize);    % 1) fft im with padding
fil_fft = fft2(fil, fftsize, fftsize);    % 2) fft fil to same size as image
im_fil_fft = im_fft .* fil_fft;           % 3) multiply fft images
im_fil = ifft2(im_fil_fft);               % 4) inverse fft2
im_fil = im_fil(1:imh, 1:imw);            % 5) remove padding

% plot
subplot(2,3,4)
imagesc(log(abs(fftshift(im_fft))+1)), colormap jet,axis off,axis equal

subplot(2,3,5)
imagesc(log(abs(fftshift(fil_fft))+1)), colormap jet,axis off,axis equal

subplot(2,3,6)
imagesc(log(abs(fftshift(im_fil_fft))+1)), colormap jet,axis off,axis equal

subplot(2,3,3)
imshow(im_fil);

subplot(2,3,1)
imshow(im)

ax1 = subplot(2,3,2);
imagesc(fil), colormap(ax1,gray),axis off,axis equal

6. 参考文献

[1] Shuman, David I., et al. “The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains.” IEEE Signal Processing Magazine.

[2] Bronstein, Michael M., et al. “Geometric Deep Learning: Going beyond Euclidean Data.” IEEE Signal Processing Magazine.

[3] Hamilton, William L. “Graph Representation Learning.” Synthesis Lectures on Artificial Intelligence and Machine Learning.

[4] Bougleux, Sébastien, et al. “Discrete Regularization on Weighted Graphs for Image and Mesh Filtering.” 1st International Conference on Scale Space and Variational Methods in Computer Vision (SSVM 2007).