Learning to Solve Hard Minimal Problems

这是 CVPR2022 的 best paper，目标是求解多视角几何中的2D-2D位姿估计问题，该问题需要求解一个代数方程，期间会产生很多伪解，需要大量规则和时间去筛选出真实解。该论文使用神经网络在给定anchor集中选取出一个合适的anchor作为起始点，然后从该起始点出发，使用同伦连续的方法获取真实解。

在 4 pt in 3 views 实验中，神经网络选对起始点的概率只有26.3%，作为对比的MINUS方法全局跟踪多个起始点，因此成功率能达到95.5%，但MINUS方法耗时 0.61 s，而该方法耗时仅 16.2 μs。考虑到问题求解都是在RANSAC框架下进行，因此可以使用平均有效时间来衡量，MINUS方法为 0.64 s，该方法为 65 μs，能达到接近10000倍的加速。

• 1. 问题背景
  • 1.1. 2D-2D位姿估计
  • 1.2. Minimal problem
  • 1.3. Previous work
• 2. Propose method
• 3. 具体细节
  • 3.1. 5pt minimal problem
  • 3.2. 神经网络
  • 3.3. 流形假设
  • 3.4. 同伦连续
  • 3.5. 其他
• 4. 推理流程
• 5. 实验结果
• 6. 代码实测
• 7. References

1. 问题背景

1.1. 2D-2D位姿估计

该论文主要面向2D到2D的位姿估计问题：

我们用同一个相机在 $O_1$ 和 $O_2$ 两点处拍照，获得了图片 $I_1,I_2$，以 $O_1$ 为标准系，$\boldsymbol{p}_1,\boldsymbol{p}_2$ 为齐次的像素坐标。我们已知相机的内参矩阵 $K$ 和像素坐标 $\boldsymbol{p}_1,\boldsymbol{p}_2$，求两个相机之间的相对位姿。

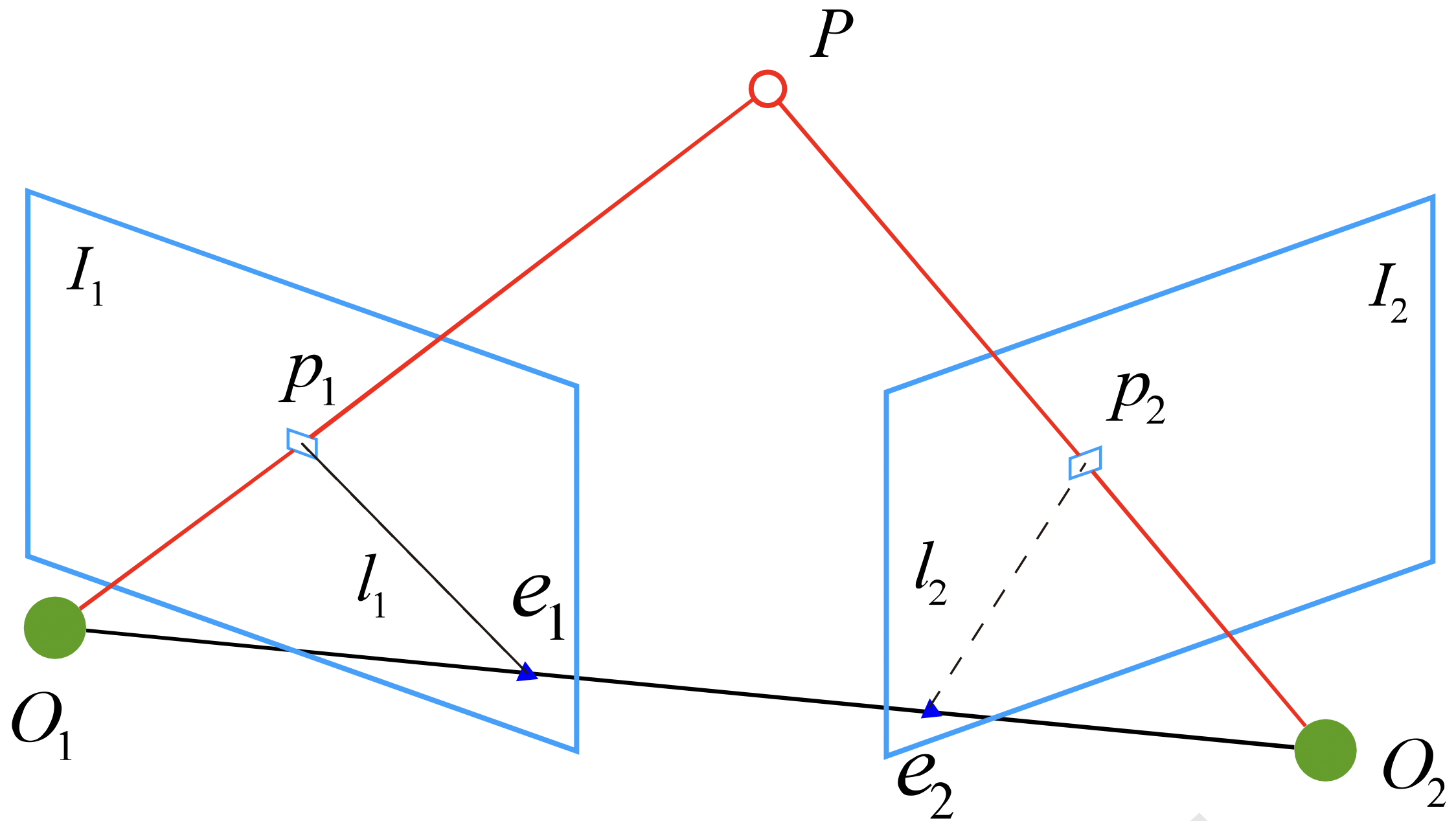
设 $P$ 在第一个相机下的坐标为

那么像素坐标与空间坐标的关系为

用$K$表示相机的内参矩阵，即

于是有

这里的 $R,\boldsymbol{t}$ 是两个相机之间的旋转矩阵和平移向量。

设 $\boldsymbol{x}_1,\boldsymbol{x}_2$ 为归一化平面上的坐标：

即

两边同时左乘 $[t]_{\times}$ 可得：

再两边同时左乘 $\boldsymbol{x}_2^{\top}$ 可得：

记 $E=[t]_{\times}R$ 为本质矩阵(Essential Matrix)，可得对极约束等式：

1.2. Minimal problem

对于上面的这个2D-2D的位姿估计问题，我们要估计本质矩阵 \(E=[t]_{\times}R\)，由于平移和旋转各有3个自由度，故 $[t]_{\times}R$ 共有6个自由度，但由于尺度等价性，因此 $E$ 实际上只有5个自由度（通常的做法是设 $t$ 的长度为1），也就是说我们最少可以用5对点来求解 $E$ 矩阵，这就是5点法。

但是我们也可以先忽略$E$的其他性质，仅考虑尺度等价性，此时$E$具有8个自由度，于是我们可以用8个点来求解 $E$ 矩阵，这就是8点法。但这样得到的矩阵不一定满足本质矩阵的性质，因此最后还需将矩阵投影到本质流形(Essential Manifold)上：

基于不同的假设，问题会有不同的自由度，当我们使用最少的输入点来解决问题时，那么这就是一个 Minimal problem，一般翻译为「最小配置问题」，更详细的解释可以参考 Zuzana Kukelova 大佬的 PhD Thesis - Algebraic Methods in Computer Vision。

Many problems in computer vision, especially problems of computing camera geometry, can be formulated using systems of polynomial equations. Such systems of polynomial equations can have an infinite number of solutions, i.e. are under-determined, no solution, i.e. are overdetermined, or these systems can have a finite number of solutions.

In the case of problems of computing camera geometry, the number of equations in the system and the corresponding number of its solutions depend on the number of geometric constraints and the number of input data (usually 2D-2D, 2D-3D or 3D-3D point or line correspondences) used to formulate the problem. The problems solved from a minimal number of input data and using all the possible geometric constrains that lead to a finite number of solutions are often called “minimal problems” or “minimal cases”. Most of these minimal problems are named according to the smallest number of correspondences that are required to solve these problems and to obtain a finite number of possible solutions, e.g., the five point relative pose problem or the six point focal length problem.

1.3. Previous work

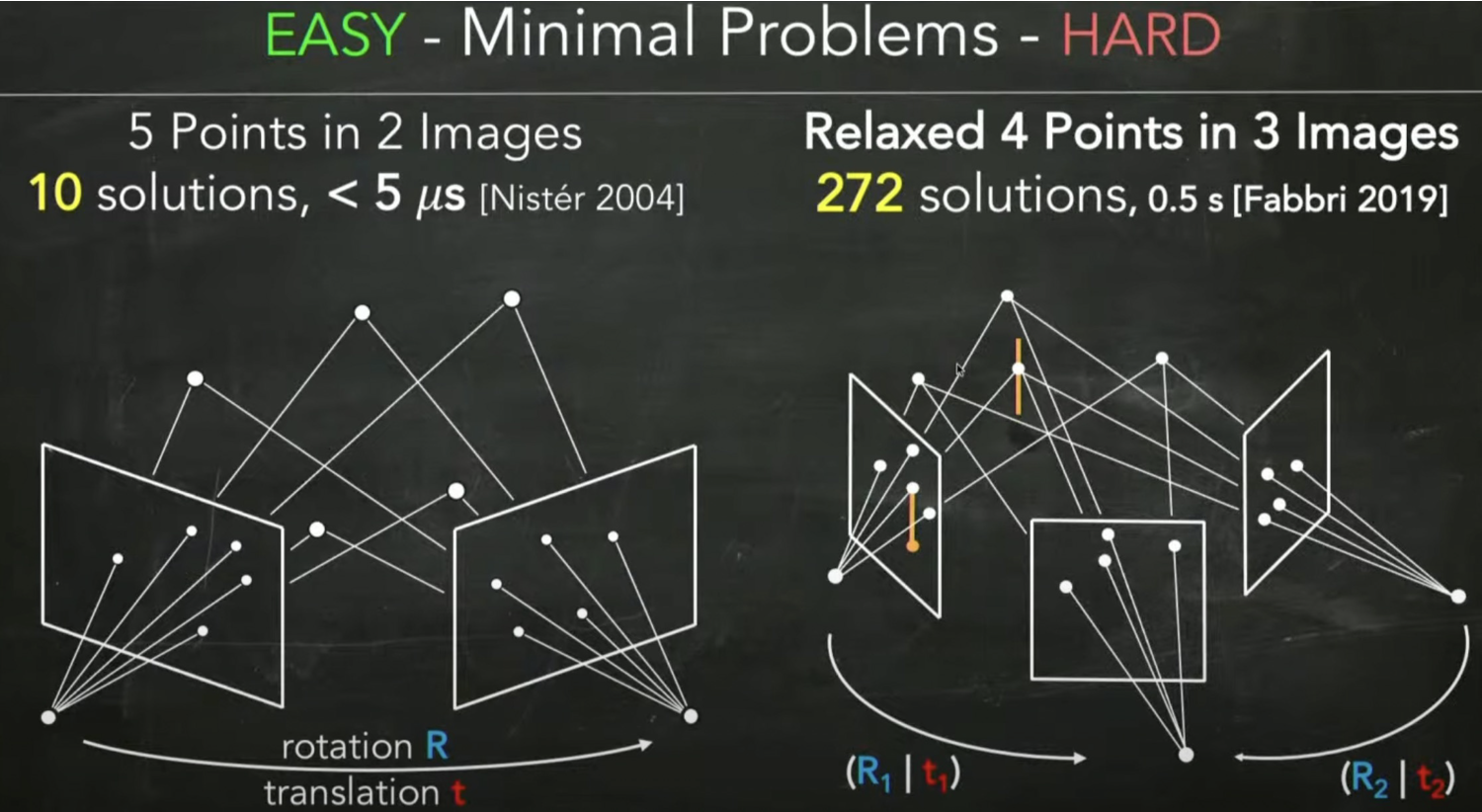
对于经典的 5-point problem (5pt)，通过5个点估计两个相机的相对位姿，虽然我们在上面列出了对极约束方程，但通过约束求解方程，还需要一系列的变形和松弛，在这个过程中会产生一系列的伪解(spurious solution)，例如我们使用Nister的5点法会得到10个解，但其中只有一个解是符合真实情况的解，剩下的9个解都是伪解，当然我们可以设定一系列的规则来判断哪些是伪解，从而将其剔除掉，使用当前最快的求解器可以在 $5\,μs$内算出全部的10个解。

但对于更复杂的问题，例如4点问题，会产生272个解，计算真实解就变得更麻烦。一般的求解器采用的是基于符号数值(symbolic-numeric)的方法：先使用 Bucheberger 算法或基于结式的方法计算 Grőbner 基，然后计算Generalized companion matrix 的特征向量得到方程的根。论文中提到，这类方法面对64个解以内的问题能稳定求解，但对于更复杂的Minimal Problem就很难得到真实解。

此外还有基于同伦连续(homotopy continuation, HC) 的方法，例如我要计算 $F(x)$ 的根，但直接计算 $F(x)$ 的根可能很困难，那么我先找到一个容易求解的 $G(x)$，然后构造 $F$ 到 $G$ 的同伦变换，例如

当 $t=0$ 时，$H(x,0)=G(x)$，此时算出根 $s_0$，然后给 $t$ 加上一个 $\Delta t$，以 $s_0$ 为初值，使用牛顿法等局部优化算法得到 $H(x,\Delta t)$ 的根 $s(\Delta t)$，以此类推，当 $t$ 从0变化到1时，我们就能得到一条解曲线 $s(t)$，此时 $s(1)$ 即为 $G(x)$ 的解。但全局HC方法需要跟踪多个解曲线以保证能找到真实解，这样的方法需要消耗大量的时间，之前的那个5pt问题，使用Macaulay2中的HC法来求解需要 $10^5\,\mu s$，通常而言，HC方法比符号数值求解器会慢1000到10万倍。

2. Propose method

HC之所以慢，就是因为它要从多个起始点开始追踪，以保证能覆盖所有的解，并且最后也要从大量伪解中选出真实解。但如果我们已经知道了真实解附近的一个起始点，那么只需要跟踪一条路径即可，这样也避免了伪解的干扰。

所以，这篇论文的核心思想就在于通过神经网络来预测一个起始点，但可以想象，直接预测一个真实解附近的起始点是比较有难度的，所以作者就先从数据集生成多个起始点，称为anchor(锚点)，然后用神经网络来推断每个问题对应的anchor，这就类似于将回归问题转化成了分类问题。

3. 具体细节

3.1. 5pt minimal problem

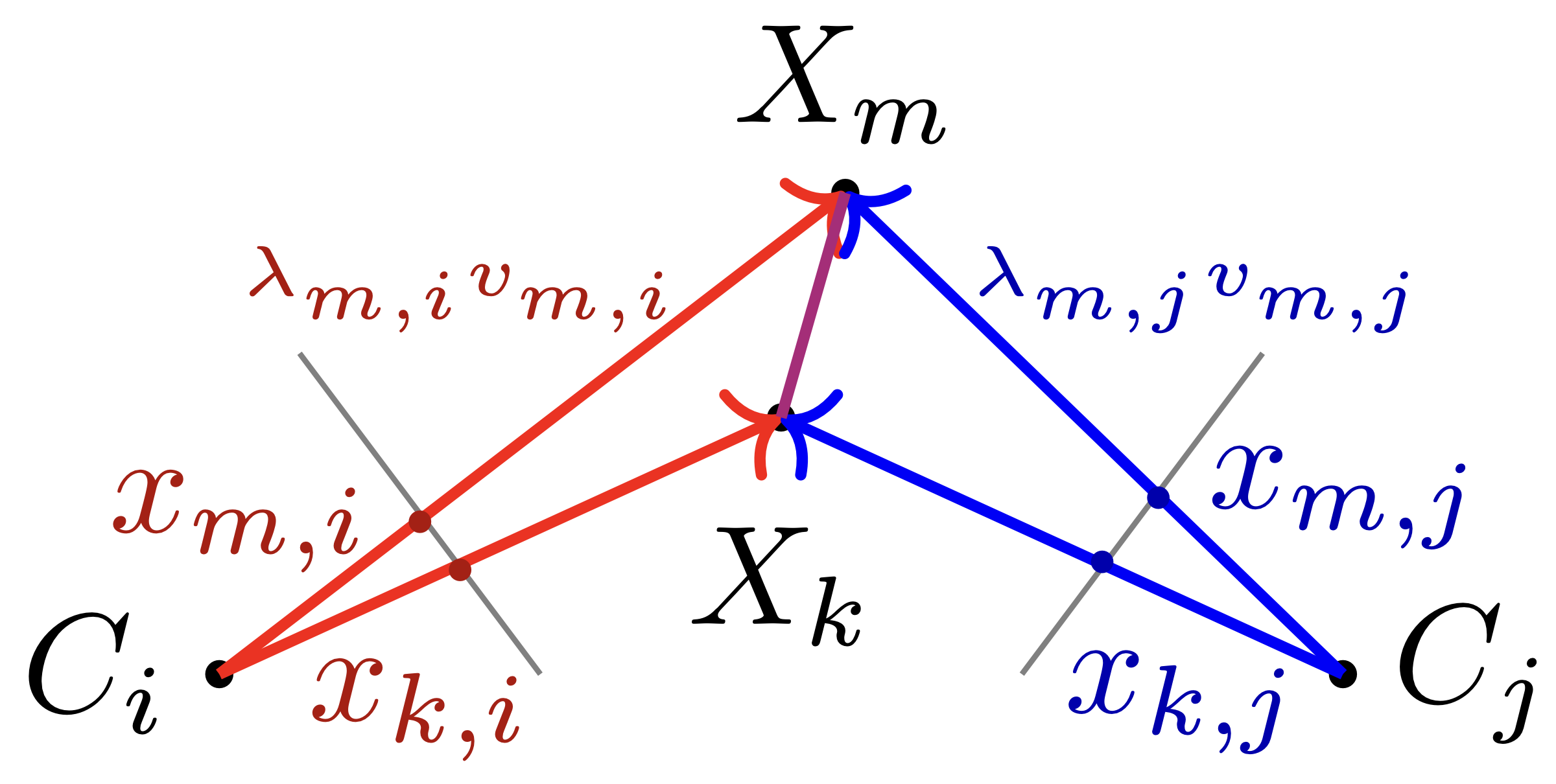
这里的问题建模与开头的不太一样，$X$ 表示空间中的3D点坐标，$C$ 表示相机，$x_{m,i}$ 表示像素点的空间坐标，$v=[x;1]$ 为 $x$ 的齐次坐标形式，$\lambda$ 为深度，$\lambda_{m,i}v_{m,i}$ 为 $X_m$ 在 $C_i$ 坐标系下的坐标。虽然$C_i$ 和 $C_j$ 之间差了个空间变换，但 $\overline{X_mX_k}$ 的长度保持不变，因此有：

假设我们选取 $n$ 个点，未知量 $\lambda$ 的个数为 $2n$，考虑到尺度不变性，我们让 $\lambda_{1,1}=1$，于是共有 $2n-1$ 个未知量。方程的个数就是边的个数，我们共可以选出 $C_n^2=n(n-1)/2$ 条边，于是需要满足

也就是说至少需要5个点，我们才能求解这个问题。而当我们只使用5个点时，这就是一个 minimal problem，也就是用最少的点解决这个问题。

关于这个问题，通常来说共有80个解，其中非奇异解有40个，在这40个非奇异解中，深度全为正且满足几何约束的解只有10个。

对于一般的HC求解器来说，只能求解方阵系统，也就是9个方程9个未知量，因此还需要舍弃一个方程。

3.2. 神经网络

神经网络的输入是一个 problem 向量 $p$ ，对于5pt问题，$p$为5个点的10个像素坐标，是一个20维的向量，这就是神经网络的输入。

网络的输出为对应anchor的序号，额外还有一个trash的label，表示该问题不属于任何anchor。

网络的结构非常简单粗暴，就是一个8层的全连接MLP。

class Net(nn.Module):
    def __init__(self, anchors):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(24, 100)
        self.relu1 = nn.PReLU(100, 0.25)
        self.fc2 = nn.Linear(100, 100)
        self.relu2 = nn.PReLU(100, 0.25)
        self.fc4 = nn.Linear(100, 100)
        self.relu4 = nn.PReLU(100, 0.25)
        self.fc5 = nn.Linear(100, 100)
        self.relu5 = nn.PReLU(100, 0.25)
        self.fc6 = nn.Linear(100, 100)
        self.relu6 = nn.PReLU(100, 0.25)
        self.fc7 = nn.Linear(100, 100)
        self.relu7 = nn.PReLU(100, 0.25)
        self.drop3 = nn.Dropout(0.5)
        self.fc3 = nn.Linear(100, anchors + 1)

    def forward(self, x):
        x = self.relu1(self.fc1(x))
        x = self.relu2(self.fc2(x))
        x = self.relu4(self.fc4(x))
        x = self.relu5(self.fc5(x))
        x = self.relu6(self.fc6(x))
        x = self.relu7(self.fc7(x))
        x = self.drop3(x)
        return self.fc3(x)

3.3. 流形假设

为什么我们能用神经网络来学习这个问题？因为这个problem-solution pair构成了一个流形，直白一点，就是problem对应的solution在大部分情况下都是连续的。

用一个三次方程 $x^3+ax+b=0$ 来举例，我们用Mathematica画出其图像，横向是由 $(a,b)$ 构成的参数平面，纵向是对应的解 $x$。

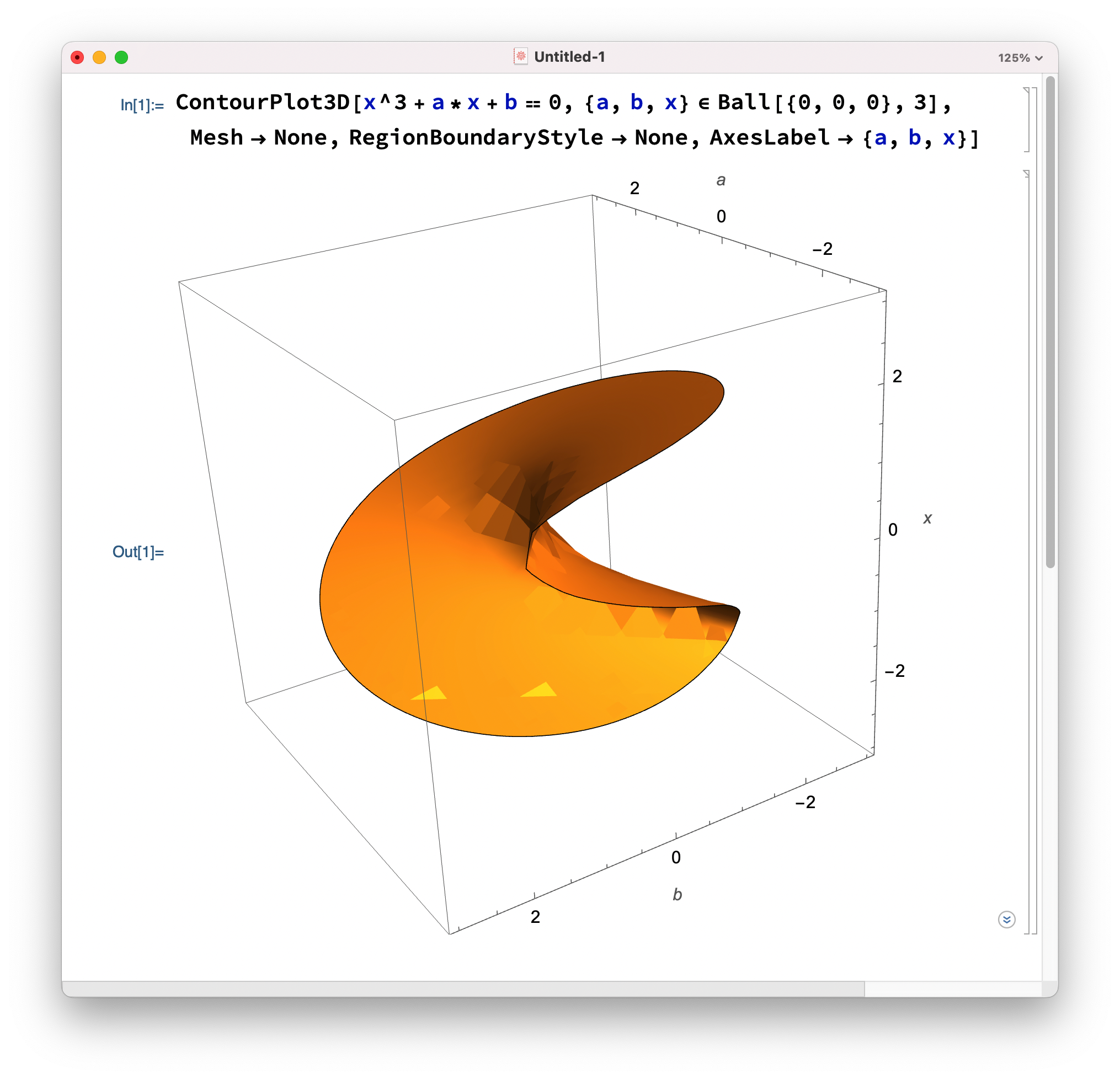
可以看到，对于不同的 $(a,b)$，对应的解 $x$ 在大部分区域内都是连续的，并且只有一个解。

但是一些特殊情况下，例如下图中的红色区域内，一个 $(a,b)$ 会对应到3个$x$，但我们很难判断这3个解中哪一个是我们真实需要的，此时就需要神经网络从数据集中学习到的先验信息来判断。

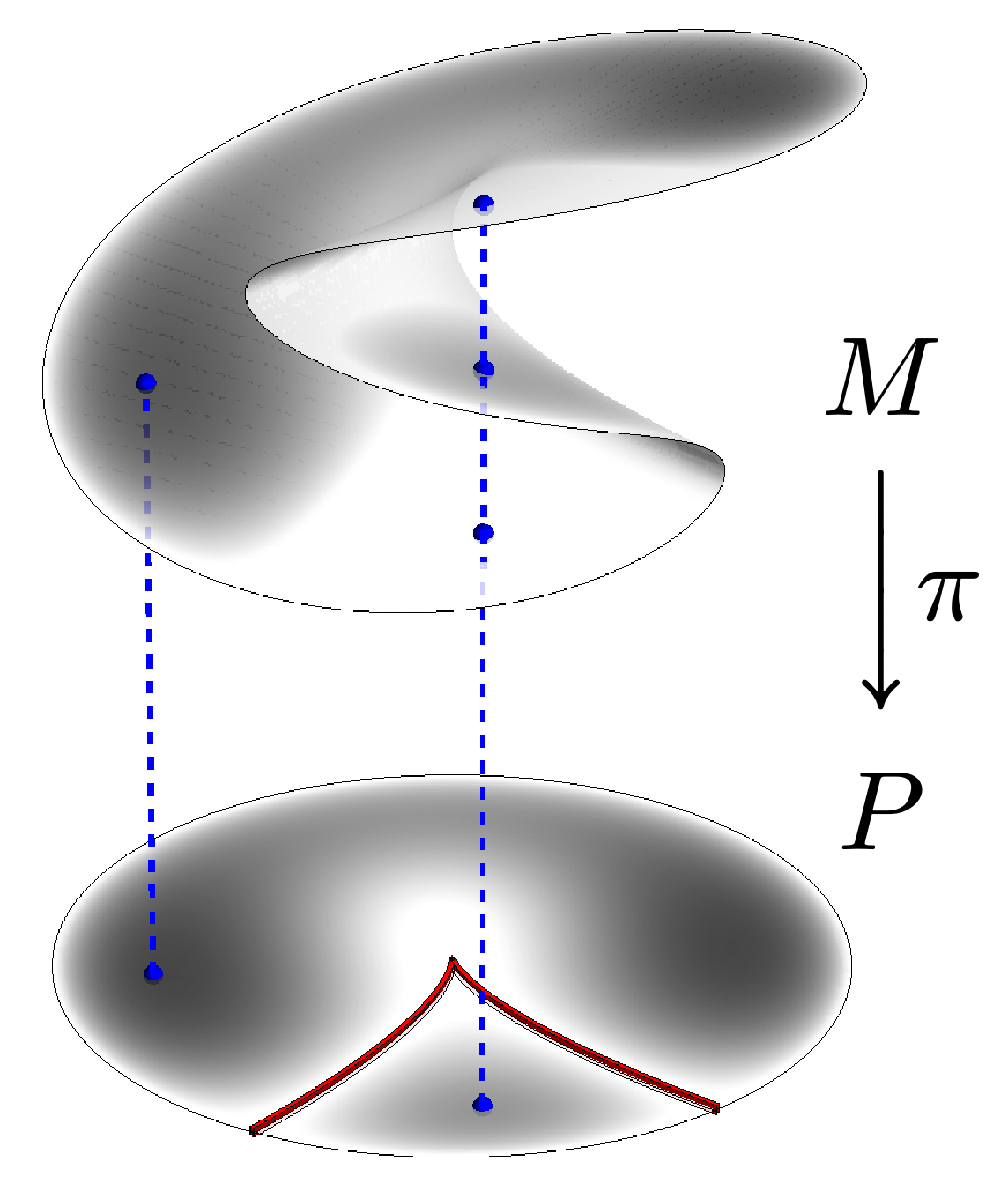
当神经网络判断出起始anchor后，我们就能用同伦连续法持续跟踪一条从起始点到目标点的曲线。

由于整个曲线都是在 problem-solution manifold 上连续变化的，因此不会出现点从上表面直接滑落到下表面的情况，这在非线性动力系统中被称为尖点灾难(cusp catastrophe)，具体可以参考Strogatz 的《Nonlinear dynamics and chaos》，这本书对 $\dot{x}=h+rx-x^3$ 这类型的分岔理论进行了详细的研究。

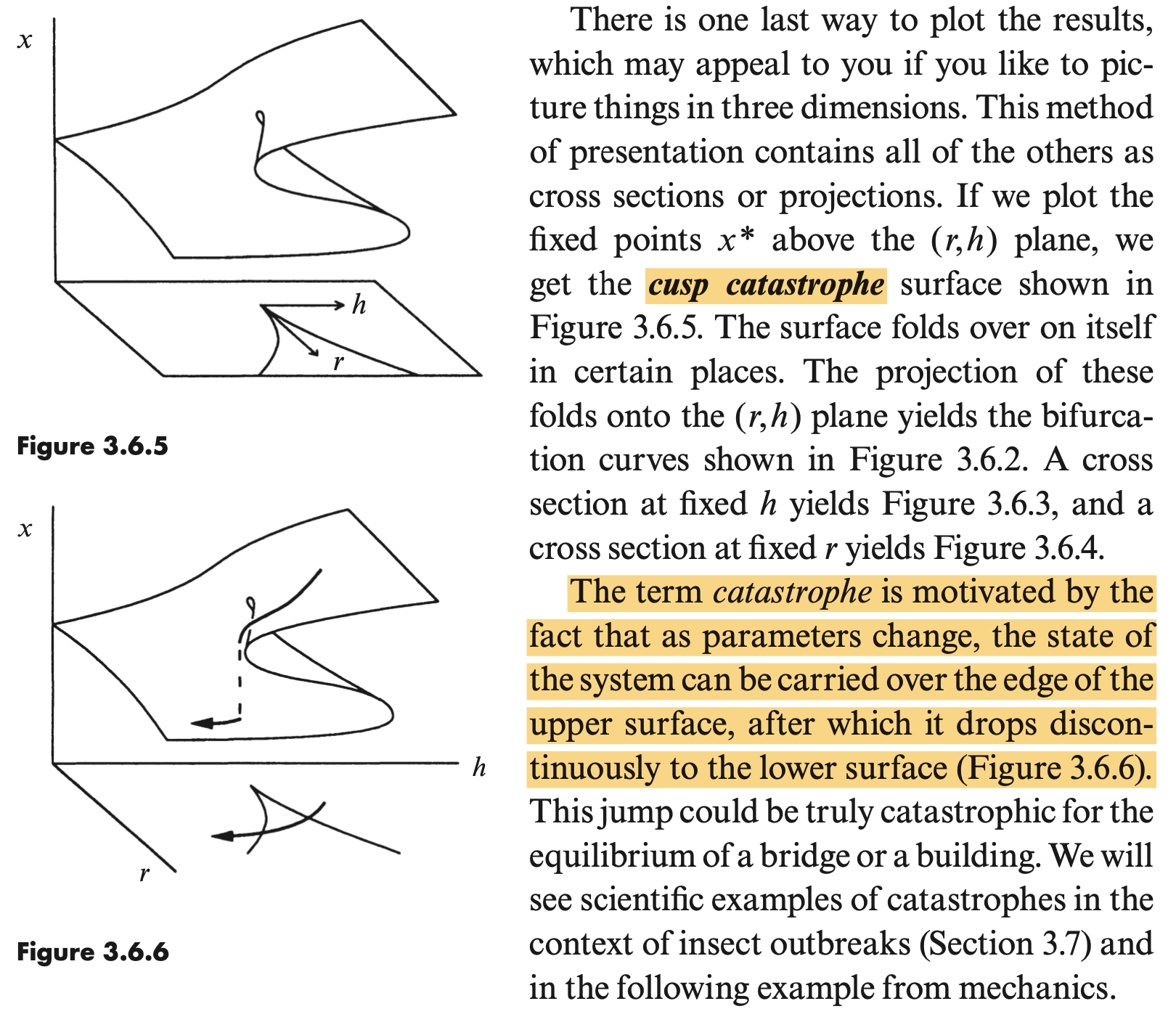
3.4. 同伦连续

如果我们要获取问题 $p$ 的解 $s$，可以先从一个已知的 problem/solution pair $(p_0, s_0)$ 出发，构建线段同伦(Linear segment HC)：

每个$t$都会对应一个解 $s(t)$，我们可以用方程组刻画隐式方程 $H(s,t)=0$ ，那么有：

对于当前点 $s(t_i)$，我们可以计算

当然这是最简单的欧拉法，实际上论文使用了更复杂的四阶Runge-Kutta法来预测 $s(t_i+\Delta t)$。

但预测步得到的$s(t_i+\Delta t)$ 不一定是 $p(t_i+\Delta t)$ 的解，因此还需要进行校正，论文中使用牛顿法，以$s(t_i+\Delta t)$作为起点，迭代3步得到更准确的解。

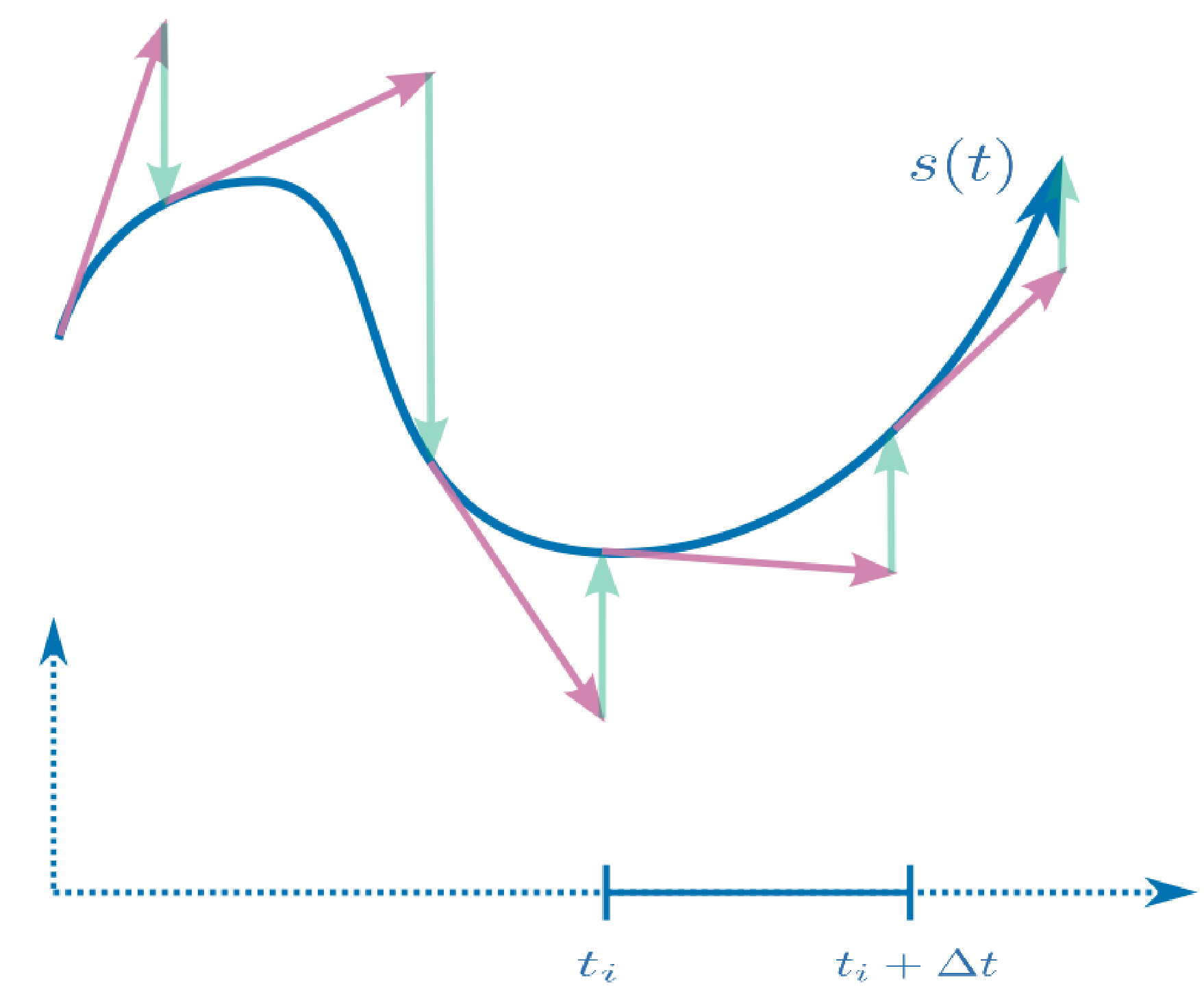
整个过程如上图所示，红色的为预测步，绿色为校正步，两者交替进行，最终得到解曲线 $s(t)$。

3.5. 其他

还有一些细节，例如 RANSAC框架、anchor集合的生成、训练集的生成，在此就不过多描述了，感兴趣的可以去看原论文。

4. 推理流程

整个推理流程还是比较明朗的

1. 将输入点转化为问题向量 $p$
2. 通过神经网络选择合适的anchor $(p_0,s_0)$
3. 构建同伦映射 $p(t)=(1-t)p_0+t(p)$
4. 从 $(p_0,s_0)$ 跟踪到 $(p,s(1))$ 得到最终解

5. 实验结果

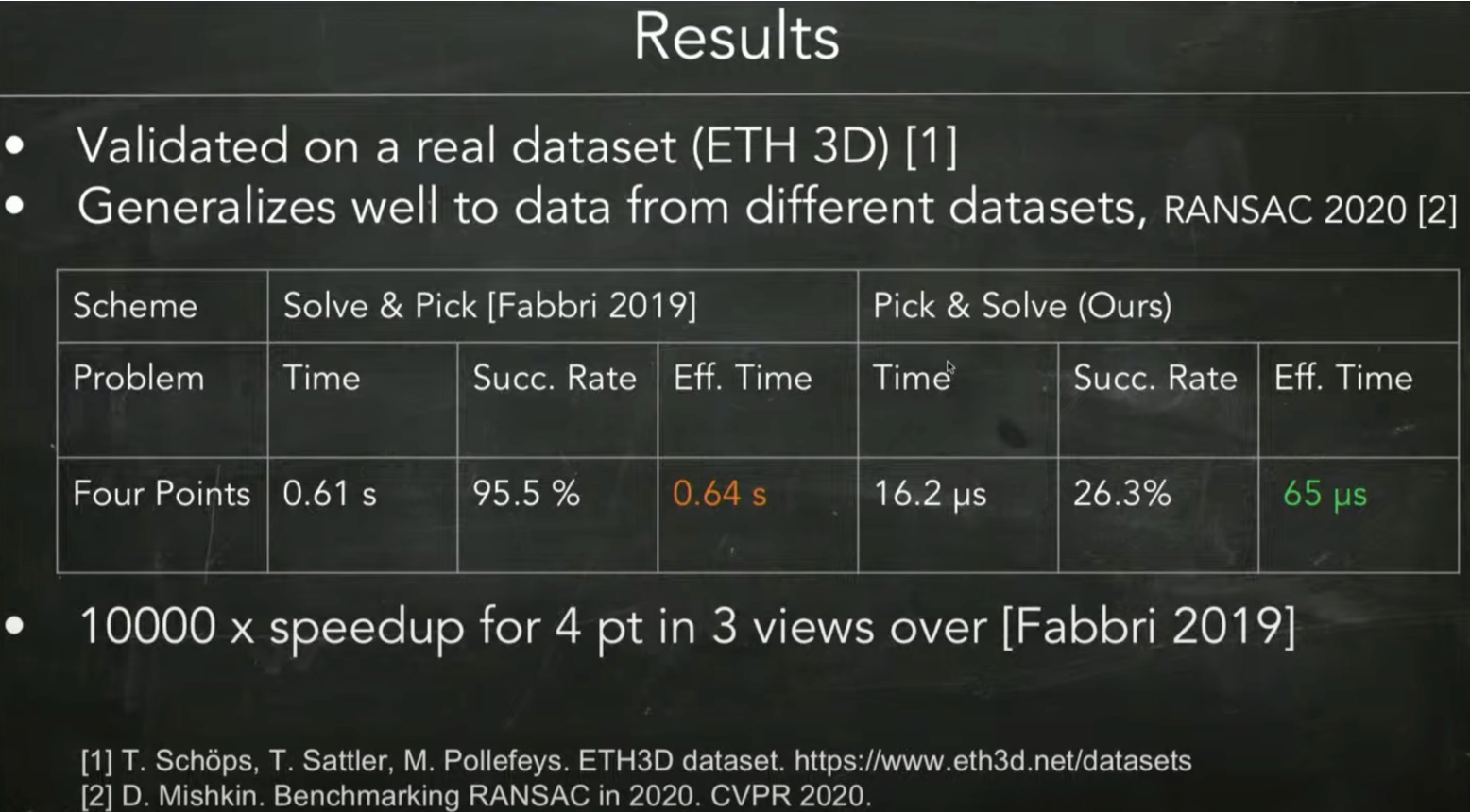
原论文的实验写得乱七八糟，这里从作者的PPT报告中粘一页图，这个 [Fabbri 2019] 就是 MINUS( MInimal problem NUmerical Solver)，这是一个基于同伦连续的通用求解器。

• MINUS是通过HC全局跟踪所有解，最终的成功率为 95%，一次的时间为 $0.61\,s$

• 论文中的方法只跟踪一个解，成功率为 26%，但用时只需 $16\, \mu s$
• 考虑到求解过程都是在 RANSAC 框架下运行，因此可以用平均有效时间来衡量，一个是 $0.64\,s$，另是 $65\,\mu s$，能达到接近 10000倍的加速

6. 代码实测

我跑了一下作者的代码，挺无语的。首先是 Readme 文档写得乱七八糟，让人摸不着头脑，然后是代码一堆BUG！！！

• Python代码有很多未定义的变量，一看就是还没检查就匆忙发布上去的
• 运行生成anchor 的脚本 ./BIN/anchors ，最终只得到了一个anchor，不知道是数据集的原因还是代码有BUG
• 尽管有人在 issue 上提出了bug，但时隔8个月依然啥都没改，现在还是只有一个 first commit

最后我辛苦改完bug，用作者给的anchor进行训练，得到结果如下

最后一行的4.189是loss，从一开始就没降下去过，我一度以为自己的训练过程是有问题的。。。

但神奇的地方来了！！！

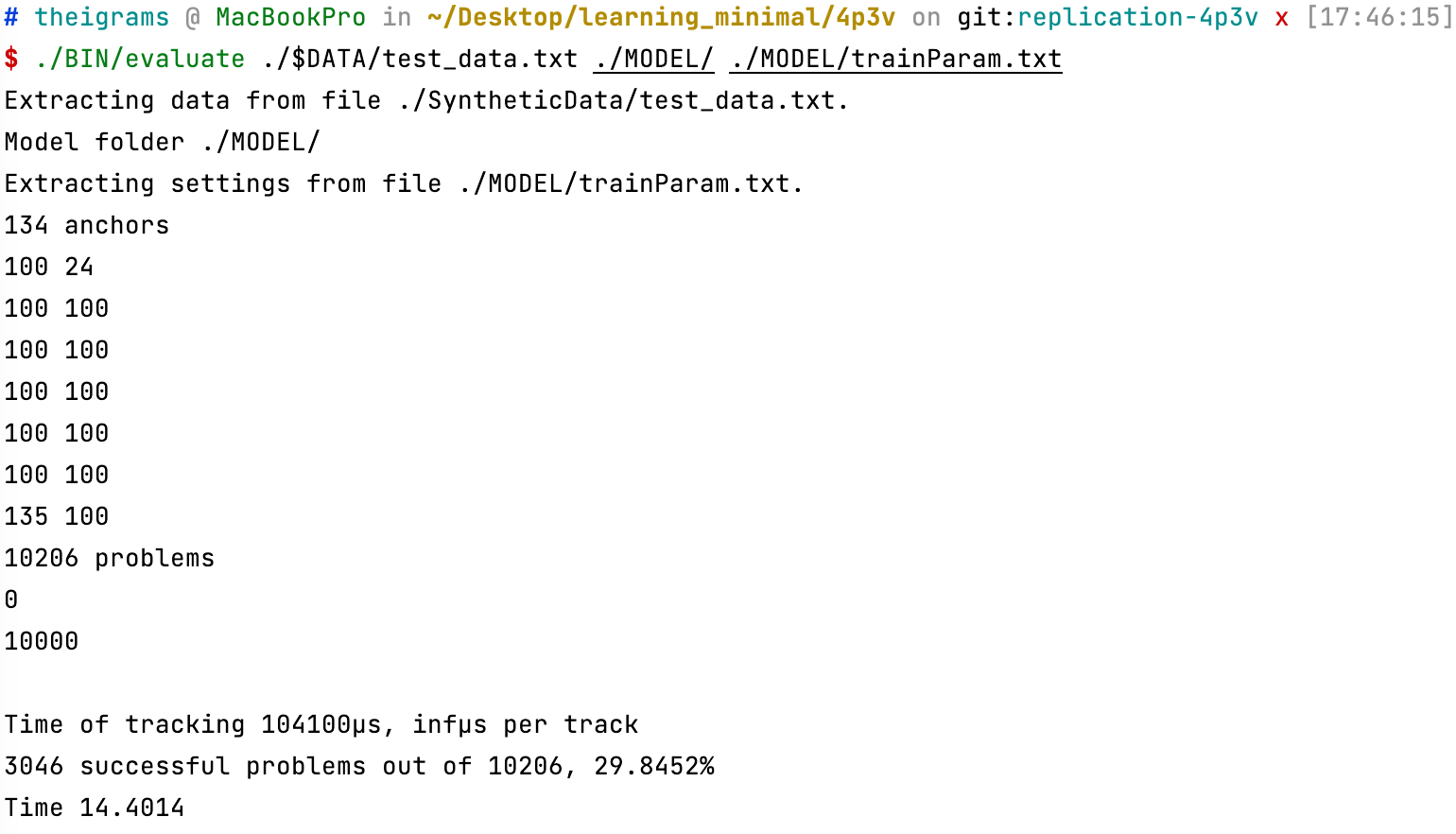
在测试集上的准确率为 28.5%，每个 tracking 用时 $14\,\mu s$，居然和论文的结果对上了。。。

以下是我的训练脚本，因为 anchor 生成那一步有问题，所以注释掉了。

set -euf

DATA="SyntheticData"
rm -rf $DATA
mkdir -p $DATA
TrainDATA="data/multi_view_training_dslr_undistorted"
TestDATA="data/multi_view_test_dslr_undistorted"

# 生成train_data
python3 sample_data.py $TrainDATA/courtyard/dslr_calibration_undistorted  $DATA/train_data_courtyard.txt 4000
python3 sample_data.py $TrainDATA/playground/dslr_calibration_undistorted  $DATA/train_data_playground.txt 1000

# 生成test_data
python3 sample_data.py $TrainDATA/relief/dslr_calibration_undistorted $DATA/test_data.txt 10000

# 生成anchor_data
python3 sample_data.py $TrainDATA/courtyard/dslr_calibration_undistorted $DATA/anchor_data.txt 10000

#如果同伦延续能够从一个问题跟踪到另一个问题，则连接两个anchor的边
./BIN/connectivity ./$DATA/anchor_data.txt ./MODEL ./MODEL/trainParam.txt

#输入是上一步生成的连接图和anchor_data，输出为最终的anchor
#./BIN/anchors ./$DATA/anchor_data.txt ./MODEL ./MODEL/trainParam.txt

# label 是生成数据集
# X_train.txt 包含训练数据的 14 维向量
# Y_train.txt 为对应的anchor的id
# 生成训练集
./BIN/labels ./$DATA/train_data_courtyard.txt ./MODEL ./$DATA train_courtyard ./MODEL/trainParam.txt
./BIN/labels ./$DATA/train_data_playground.txt ./MODEL ./$DATA train_playground ./MODEL/trainParam.txt

# 将来自不同数据集的训练集合并
cat ./$DATA/X_train_courtyard.txt ./$DATA/X_train_playground.txt > ./model/X_train.txt
cat ./$DATA/Y_train_courtyard.txt ./$DATA/Y_train_playground.txt > ./model/Y_train.txt

# 生成测试集
./BIN/labels ./$DATA/test_data.txt ./MODEL ./MODEL val ./MODEL/trainParam.txt

# 训练
python3 train_nn.py ./MODEL ./MODEL/trainParam.txt

# 验证
./BIN/evaluate ./$DATA/test_data.txt ./MODEL/ ./MODEL/trainParam.txt

这里我用 courtyard 和 playground 作为训练集，用 relief 作为测试集，机器为MBP14。

即使我将网络设置随机权重，准确率仍有19%，所以感觉这个网络其实也没学到多少东西。

整体看下来，作者的思想还是可以的，但神经网络的设计仍有待提升。

7. References

1. 相对位姿估计的进展和新方法
2. Minimal problem
3. 作者在CVPR上的报告
4. Zuzana Kukelova 的主页
5. GitHub - petrhruby97/learning_minimal: Learning to Solve Hard Minimal Problems