泊松曲面重建
泊松曲面重建(Poisson Surface Reconstruction, PSR) 是Lorensen在2006年提出来的一种三维重建方法,其将点云转换为隐式表达的曲面,然后通过Marching Cubes等方法将隐式曲面转换为网格表示。 本文的PDF版可在这里下载。
1. 泊松重建理论
泊松曲面重建(Poisson Surface Reconstruction, PSR) 是Lorensen在2006年 提出来的一种三维重建方法,其将点云转换为隐式表达的曲面,然后通过Marching Cubes等方法将隐式曲面转换为网格表示。
1.1. 指示函数
和之前的很多工作一样,这里也使用了3D指示函数(indicator function)来表示曲面:
\[\chi_M(p)=\left\{ \begin{array}{ll} 1, & p\in M\\ 0, & p\notin M \end{array} \right.\]当点$p$在曲面$M$内部时,$\chi_M(p)=1$;当点$p$在曲面$M$外部时,$\chi_M(p)=0$。那么我们只需要能拟合出$\chi_M(p)$函数,就可以表示出曲面$M$。
但是直接拟合$\chi_M(p)$函数是非常困难的,因此作者提出拟合$\chi_M(p)$的梯度场函数$\nabla \chi_M$,由于$\chi_M$在曲面内部和外部区域都是常数,所以$\nabla \chi_M$在曲面内部和外部区域都是零向量,仅在曲面边界上有非零值。
另一方面,指示函数的梯度方向跟曲面的法线方向应该是一致的,也就是说我们需要最小化梯度场$\nabla \chi$ 和法向量场$\vec{V}$的差异,即最小化以下能量函数:
\[E(\chi)=\int_M \left\| \nabla \chi(p)-\vec{V}(p) \right\|^{2} \mathrm{d} p \tag{1} \label{eq:poisson1}\]其中$\vec{V}$表示点云的法向量场,如图 1所示。

Figure 1:指示函数的梯度方向应该跟曲面的法线方向是一致的。
1.2. 定义梯度场
由于$\chi_M$在曲面外到曲面上的过渡是突变的,如果严格计算$\chi_M$的导数的话,那么其导数在曲面上的值为无穷大。为了避免这种情况,作者提出了一种定义梯度场的方法:即先对$\chi_M$进行平滑处理,然后计算平滑后的$\chi_M$的导数。这里的平滑处理使用了一个高斯滤波器,即:
\[\tilde{F}(r)=\frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{r^{2}}{2\sigma^{2}}\right)\]其中$\sigma$是一个参数,用来控制平滑程度。那么对于点$p$,在其周围$q$处的高斯权重为:
\[\tilde{F}_p(q)=\tilde{F}(q-p)\]对于点$p$,使用高斯滤波器对$\chi_M(p)$进行平滑后,其值为邻域点的高斯加权平均值:
\[\begin{aligned} (\chi_M * \tilde{F})(p) &=\int \tilde{F}(p-q) \chi_M(q) \mathrm{d} q\\ &=\int_{M} \tilde{F}_p(q) \mathrm{d} q \\ \end{aligned}\]平滑后的梯度场计算公式为:
\[\nabla \left( \chi_M * \tilde{F} \right) (q_0)=\int_{\partial M} \tilde{F}_p(q_0) \vec{N}_{\partial M}(p) \mathrm{d} p \tag{2} \label{eq:poisson}\]其中$\vec{N}_{\partial M}(p)$是点$p\in \partial M$的法向,其方向指向曲面内部。Equation $\eqref{eq:poisson}$的详细证明见 附录。
1.3. 近似梯度场
Equation $\eqref{eq:poisson}$是一个连续的积分方程,这里作者使用法向量的离散采样来近似。对于输入点云数据$S$,其中的每个元素$s$都有一个法向量$s.\vec{N}$和一个点坐标$s.p$。根据$s$将曲面$\partial M$ 划分成不相交的局部区域 $\mathscr{P}_s$,然后积分方程可近似为:
\[\label{eq:poss2} \begin{aligned} \nabla\left(\chi_M * \tilde{F}\right)(q) & =\sum_{s \in S} \int_{\mathscr{P}_s} \tilde{F}_p(q) \vec{N}_{\partial M}(p) \mathrm{d} p \\ & \approx \sum_{s \in S} \int_{\mathscr{P}_s} \tilde{F}_{s.p}(q) \vec{N}_{\partial M}(s.p) \mathrm{d} s.p \\ & \approx \sum_{s \in S}\left|\mathscr{P}_s\right| \tilde{F}_{s.p}(q) s.\vec{N} \equiv \vec{V}(q) \end{aligned}\]第二行用$s.p$代替了$p$,第三行用$\mathscr{P}_s$的面积$|\mathscr{P}_s|$代替了$\mathrm{d} p$的积分。
当$S$为均匀分布的点云时,$|\mathscr{P}_s|$为固定的常数,可以忽略不计,此时有
\[\vec{V}(q) \approx \sum_{s \in S} \tilde{F}_{s.p}(q) s.\vec{N} \tag{3} \label{eq:smooth}\]也就是将法向量场$\vec{V}$近似为采样点$s$法向量的加权平均,如图 2所示。
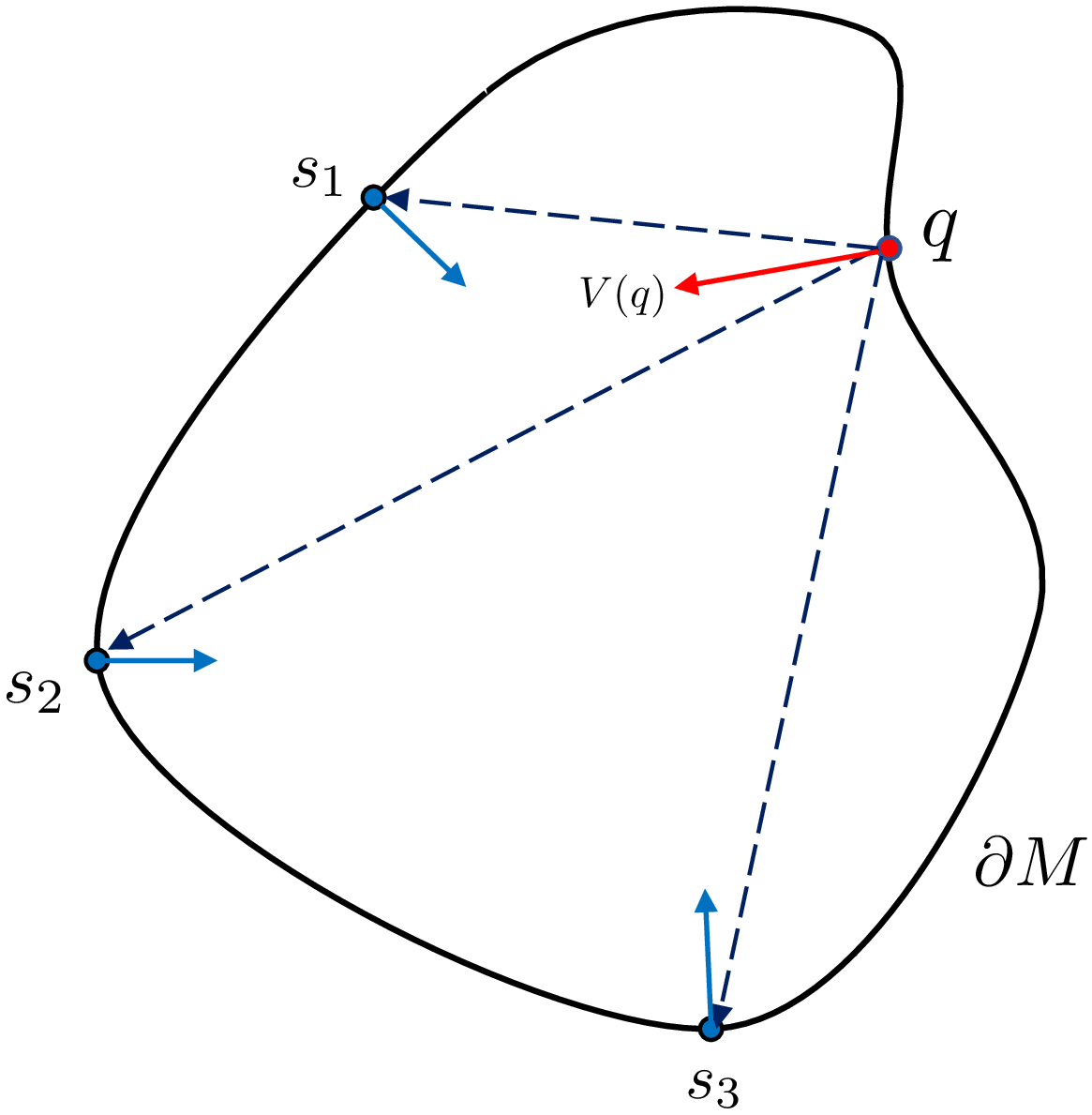
Figure 2: $\vec{V}(q)$可以近似表示成周围采样点法向$s.\vec{N}$的高斯加权平均
1.4. 求解泊松方程
经过上面的处理,我们得到了法向量场$\vec{V}$的近似表达式,接下来我们希望最小化梯度场$\nabla \chi$ 和法向量场$\vec{V}$的差异,即最小化式$\eqref{eq:poisson1}$的能量函数,但问题在于$\vec{V}$并不是可积的,因此转而最小化$\nabla \cdot \vec{V}$和$\nabla \cdot \nabla \chi=\Delta \chi$的差异,即:
\[\min_{\chi} \int_{M} \left(\nabla \cdot \vec{V} - \Delta \chi\right)^2 \mathrm{d} p\]1.5. 自适应八叉树
在具体的实现时,为了减少计算量,需要使用自适应八叉树(Adaptive Octree)的数据结构。对于点集$S$和八叉树$\mathscr{O}$,我们设定八叉树的最大深度为$D$,然后可以构建自适应的划分,使得每个采样点$s$都落在深度为$D$的叶子节点中。
八叉树中的每一个节点$o$都是三维空间中的一个立方体,其中心位置为$o.c$,边长为$o.w$。对于每个节点$o$,我们可以定义一个节点函数$F_o$,使得
\[F_o(q) =F\left( \frac{q-o.c}{o.w} \right) \frac{1}{o.w^3}\]这里 $F$为标准高斯分布,也就是说$F_o$是一个以$o.c$为中心,$o.w$为标准差的高斯分布。
此时,我们希望用一系列节点函数${F_o}$来表示向量场$\vec{V}$,观察式$\eqref{eq:smooth}$,我们知道向量场可近似表示为采样点法向的加权平均:
\[\vec{V}(q) \approx \sum_{s \in S} \tilde{F}_{s.p}(q) s.\vec{N}\]在自适应八叉树数据结构中,我们知道$s.p$会落在一个深度为$D$的叶子节点中,假设节点为$o$,那么我们可以用节点的中心$o.c$来近似代替$s.p$,那么有
\[\begin{aligned} \vec{V}(q) &\approx \sum_{o \in \mathscr{O}} \tilde{F}_{o.c}(q) s.\vec{N}\\ & = \sum_{o \in \mathscr{O}} \tilde{F}(q-o.c) s.\vec{N} \end{aligned}\]由于滤波函数$\tilde{F}$是对周围的网格进行卷积,其尺度也跟网格宽度一个级别,其标准差为$2^{-D}$,即有
\[F(q)=\tilde{F}\left(\frac{q}{2^D}\right)\]但是仅用网格中心代替采样点仍有不小误差,为了进一步提高精度,作者使用三线性插值来近似,即
\[\vec{V}(q) \equiv \sum_{s \in S} \sum_{o \in \operatorname{Ngbr}_D(s)} \alpha_{o, s} F_o(q) s.\vec{N}\]这里 \(\operatorname{Ngbr}_D(s)\) 是离$s.p$最近的八个深度为$D$的邻居节点,$\alpha_{o, s}$是插值权重。
1.6. 泊松方程的矩阵描述
在上面,我们已经将$\vec{V}$用$F_o$来表示,接下来我们将 $\chi$ 也用$F_o$来表示:
\[\tilde{\chi}=\sum_o x_o F_o\]这里的$x_o$是未知的系数。
我们要求解$\nabla \cdot \vec{V} =\Delta \chi$,等价于求解$\tilde{\chi}$最小化 $\nabla \cdot \vec{V}$和$\Delta \chi$在$F_o$上投影的差异:
\[\sum_{o \in \mathscr{O}}\left\|\left\langle\Delta \tilde{\chi}-\nabla \cdot \vec{V}, F_o\right\rangle\right\|^2=\sum_{o \in \mathscr{O}}\left\|\left\langle\Delta \tilde{\chi}, F_o\right\rangle-\left\langle\nabla \cdot \vec{V}, F_o\right\rangle\right\|^2 .\]我们将其转换为矩阵形式:
\[\min _{x \in \mathbb{R}^{|\sigma|}}\|L x-v\|^2 .\]其中的$v$是一个$| \mathscr{O} |$维的向量$v$,其中第$o$个元素为$v_o=\left\langle\nabla \cdot \vec{V}, F_o\right\rangle$。这里的$L$是一个$|\mathscr{O}| \times |\mathscr{O}|$的矩阵,使得$Lx$的结果为$\Delta \tilde{\chi}$在基函数${F_o}$上的投影。具体而言,$L$矩阵的第$\left(o, o^{\prime}\right)$个元素的值为
\[L_{o, o^{\prime}} \equiv\left\langle\frac{\partial^2 F_o}{\partial x^2}, F_{o^{\prime}}\right\rangle+\left\langle\frac{\partial^2 F_o}{\partial y^2}, F_{o^{\prime}}\right\rangle+\left\langle\frac{\partial^2 F_o}{\partial z^2}, F_{o^{\prime}}\right\rangle .\]注意这里的$L$是一个对称矩阵,因此原方程可以通过共轭梯度法求解。
1.7. 表面提取
在求解泊松方程得到$\tilde{\chi}$之后,我们需要将其转换为显示曲面,可以将$\tilde{\chi}(q)=r$的点都提取出来,就得到了一个等值面:
\[\partial \tilde{M} \equiv\left\{q \in \mathbb{R}^3 \mid \tilde{\chi}(q)=\gamma\right\} \quad \text { with } \quad \gamma=\frac{1}{|S|} \sum_{s \in S} \tilde{\chi}(s \cdot p)\]这里的$r$取所有数据点的平均值,可以看到缩放$\tilde{\chi}$并不会改变提取的表面。
在提取出等值面以后,就可以使用Marching Cubes等方法将等值面转换为显式网格。
1.8. 非均匀情况
前面都是基于点云均匀分布的情况,对于非均匀的点云,作者提出了一个密度权重项:
\[W_{\hat{D}}(q) \equiv \sum_{s \in S} \sum_{o \in \operatorname{Ngbr}_{\hat{D}}(s)} \alpha_{o, S} F_o(q)\]其中$\hat{D} \leq D$是一个预先给定的深度,这里是计算$\hat{D}$深度节点中的所有节点函数的三线性插值。
由于面积与采样密度成反比,所以法向量场可重新表示为:
\[\vec{V}(q) \equiv \sum_{s \in S} \frac{1}{W_{\hat{D}}(s.p)} \sum_{o \in \operatorname{Ngbr}_D(s)} \alpha_{o, s} F_o(q)\]由于节点函数的深度越小,光滑滤波的带宽越大,上式可进一步修改为
\[\vec{V}(q) \equiv \sum_{s \in S} \frac{1}{W_{\hat{D}}(s.p)} \sum_{o \in \operatorname{Ngbr}_{\text {Depth}(s. p)}(s)} \alpha_{o, s} F_o(q) .\]这里的$\operatorname{Depth}(s.p)$表示采样点$s \in S$的期望深度,它由$s.p$处的密度与平均密度的相对值确定:
\[\operatorname{Depth}(s.p) \equiv \min \left(D, D+\log _4\left(W_{\hat{D}}(s.p) / W\right)\right)\]最终提取表面时,使用指示函数的面积加权平均:
\[\partial \tilde{M} \equiv\left\{q \in \mathbb{R}^3 \mid \tilde{\chi}(q)=\gamma\right\} \quad \text { with } \quad \gamma=\frac{\sum \frac{1}{W_{\hat{D}}(s \cdot p)} \tilde{\chi}(s \cdot p)}{\sum \frac{1}{W_{\hat{D}}(s \cdot p)}}\]2. 重建总流程
2.1. 点云数据
这里我们使用经典的Bunny模型进行实验,首先通过泊松圆盘采样得到5000个点的点云数据,然后添加均值为0,标准差为0.001的高斯噪声,作为重建流程的输入点云,如图 4所示。
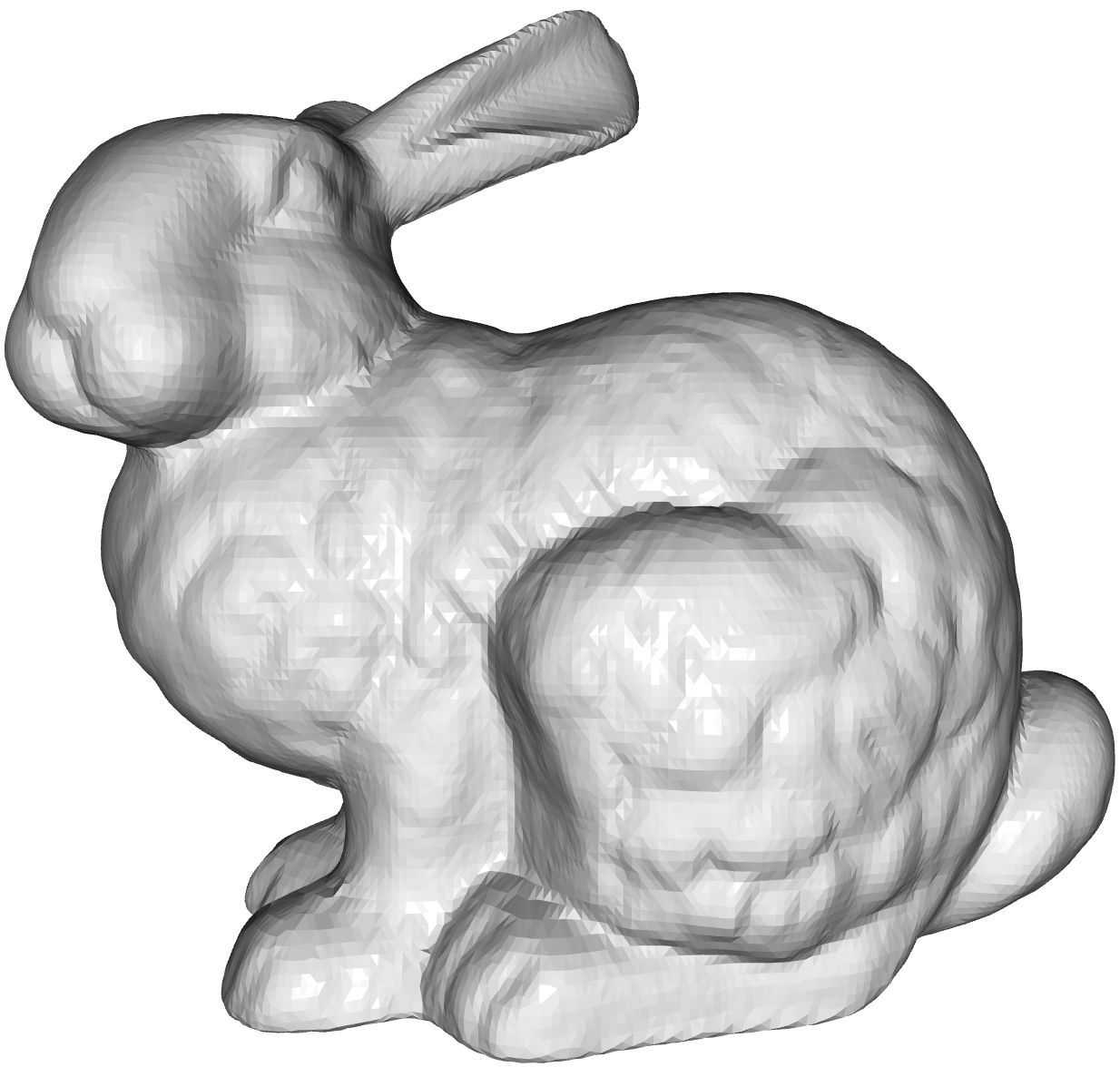

Figure 3: (左)初始Bunny模型;(右)泊松圆盘下采样后的点云
2.2. 点云处理
2.3. 体素网格采样
体素网格下采样是将空间分成一个个边长为$r$的立方体网格,然后将每个网格中的点云取平均值,作为下采样点云。具体流程如下:
-
计算点集 \(\left\{p_{1}, p_{2}, \cdots p_{N}\right\}\)的边界
\[x_{\max }=\max \left(x_{1}, x_{2}, \cdots, x_{N}\right),\quad x_{\min }=\min \left(x_{1}, x_{2}, \cdots, x_{N}\right),\quad y_{\max }=\cdots \cdots\] -
根据点集的范围划分体素网格的尺寸$r$
-
计算体素网格的维数
\[\begin{array}{l} D_{x}=\left(x_{\max }-x_{\min }\right) / r \\ D_{y}=\left(y_{\max }-y_{\min }\right) / r \\ D_{z}=\left(z_{\max }-z_{\min }\right) / r \end{array}\] -
计算每个点所属网格的编号
\[\begin{aligned} h_{x} &=\left\lfloor\left(x-x_{\min }\right) / r\right\rfloor \\ h_{y} &=\left\lfloor\left(y-y_{\min }\right) / r\right\rfloor \\ h_{z} &=\left\lfloor\left(z-z_{\min }\right) / r\right\rfloor \\ h &=h_{x}+h_{y} *D_{x}+h_{z}* D_{x} * D_{y} \end{aligned}\] -
根据步骤4中的索引对点进行排序
-
遍历所有点,对同一网格中的点取平均,得到下采样点云
在点云数量非常多的情况下,$O(n\log n)$时间复杂度的排序也需要消耗不少时间,此时可以通过哈希映射的方法进行非精确的近似下采样。

Figure 4: (左)噪声点云;(右)体素网格下采样后的点云
2.4. 去除离群点
常见的去除离群点的方法有两种,一种是基于半径的,另一种方法是基于统计的。
2.4.1. Radius Outlier Removal
-
对于每个点,找到 $r$ 半径内的邻居点
-
统计邻居点个数 $k$,如果 $k<k^*$,那么认为是离群点
这种方法的缺陷是需要给定三个参数$r,k$和$k^*$。
2.4.2. Statistical Outlier Removal
-
对于每个点$i$,划分一个邻域,找到邻域内的邻居点
-
计算到所有邻居点$j$的距离 $d_{ij}$
-
假设距离服从高斯分布 $d\sim N\left( \mu ,\sigma \right)$ 进行建模,计算参数
\[\mu =\frac{1}{nk}\sum_{i=1}^n{\sum_{j=1}^k{d_{ij}}}\] \[\sigma =\sqrt{\frac{1}{nk}\sum_{i=1}^n{\sum_{j=1}^k{\begin{array}{c} \left( d_{ij}-\mu \right) ^2\\ \end{array}}}}\] -
如果 $\mu -3\sigma <d_i<\mu +3\sigma$,那么认为属于正常点,否则就是离群点
这个比基于噪声的方法更实用,只需确定合适的$k$即可,这里我们使用基于统计的方法去除离群点,效果如图 5所示:
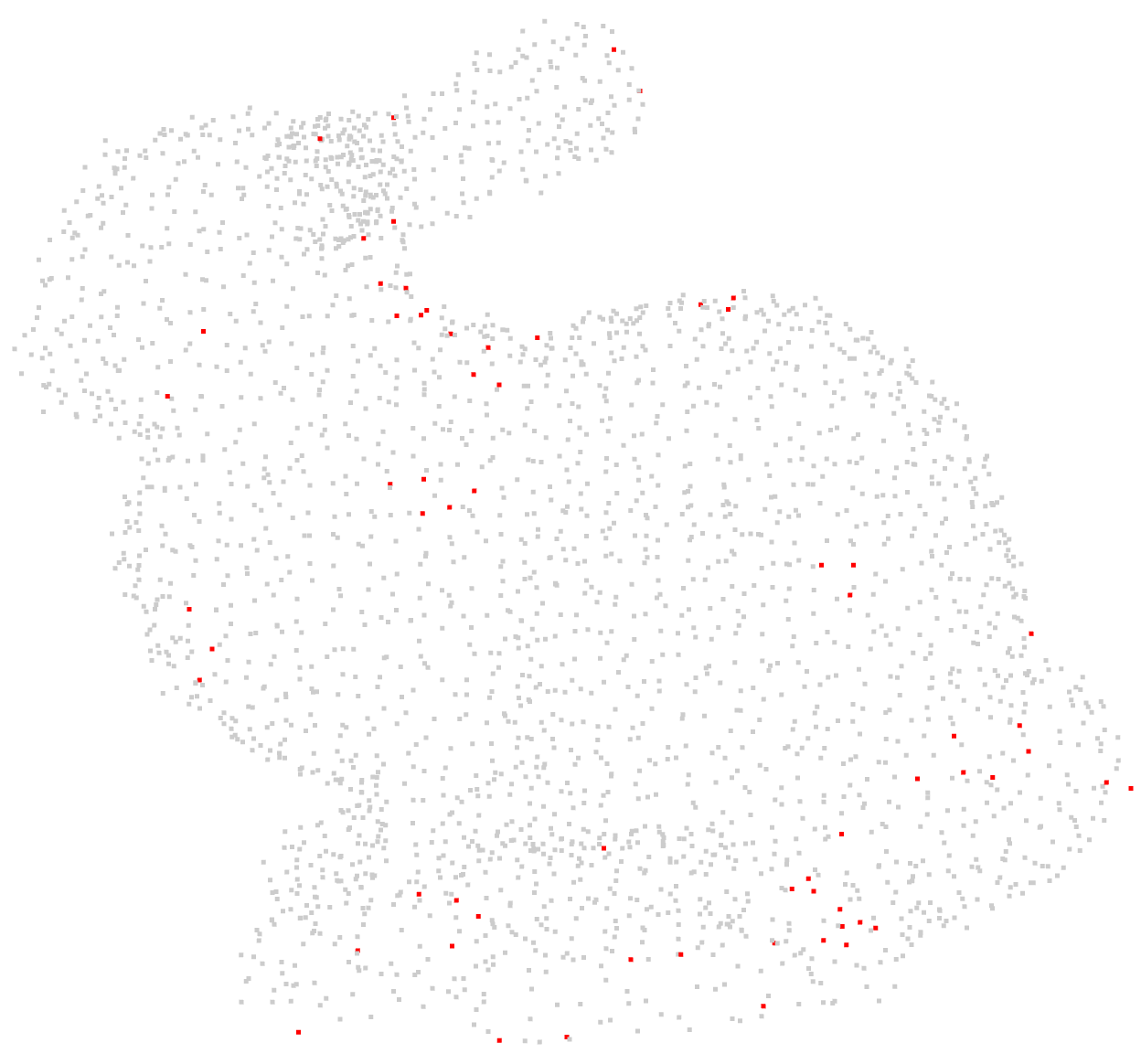
Figure 5: 这里的灰点为内点,红点为算法判定的离群点
2.5. 法向估计
由于泊松重建需要点云的法向信息,因此我们还需要对点云的法向进行估计。
2.5.1. PCA法线估计
法线估计一般使用PCA算法:先建立$k$-d 树,对于给定的点$x_i\in \mathbb{R}^3$,可以快速找到最近的$k$个邻居点组成 $X=\left[ x_1,x_2,\cdots x_k \right] \in \mathbb{R}^{3\times k}$,显然,这些点在法向量方向上投影的方差最小,因此我们可以用协方差矩阵 $XX^{\top}$的最小特征值所对应的特征向量来作为法向量的估计。
2.5.2. 法线定向
用PCA估计出法线后,这里的法线是没有方向的,我们需要对法线进行重新定向,使得法线全部朝外。这里一般使用法向传播算法:
-
将点云中每个点$p_i$作为图的顶点,将图的边的权重赋值为 $w_{ij}=1- |\boldsymbol{n}_i \cdot$ $\boldsymbol{n}_j |$, 其中 $\boldsymbol{n}_i,\boldsymbol{n}_j$ 分别 $\left(p_i, p_j\right)$ 对应的法向,这样就构成了一张黎曼图;
-
计算黎曼图的最小生成树;
-
将该黎曼图的关联顶点作为起始点, 并以该 点法向方向为参考法向, 遍历黎曼图最小生成树并 进行法向传播。若 $\boldsymbol{n}_i \cdot \boldsymbol{n}_j<0$, 则对法向进行翻转。
其效果如图 6所示。


Figure 6: (a)PCA估计法向;(b)法向定向;可以看到,定向后的法向具有更好的一致性
2.6. 泊松重建
由于泊松重建的代码实现非常复杂,
因此我们这里选择直接调用Open3D中内置的泊松重建函数
create_from_point_cloud_poisson(),其重建效果如图 7所示。
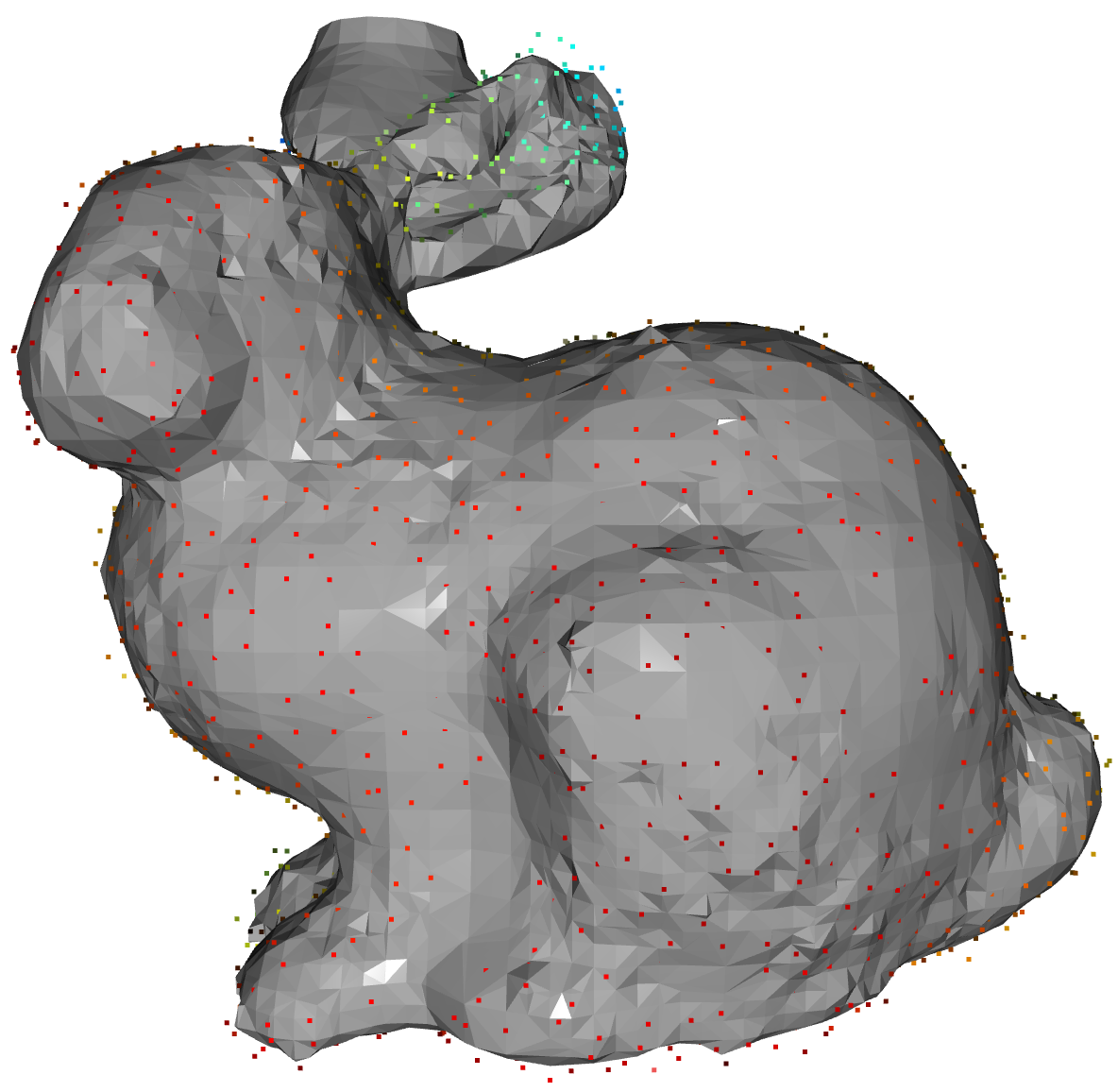
Figure 7: 泊松重建得到的网格曲面,彩色的点为泊松重建的输入点云
对于非均匀分布的点云,泊松重建算法还会计算每个点的密度作为自适应权重,这里我们将密度也可视化出来,可以看到在图 8中,兔子的右耳处密度较低,该区域的重建效果也相对差一些。

Figure 8: 泊松重建的密度区域可视化,紫色表示低密度,黄色表示高密度
此外,泊松重建使用了自适应八叉树数据结构,这里我们也将其进行了简单的可视化,如图 9所示。

Figure 9: 泊松重建的八叉树可视化(图中演示的八叉树最大深度为5,而在泊松重建中我们使用的最大深度为8)
附录:式(6)的证明
我们先计算$\left( \chi_M * \tilde{F} \right)$关于$x$坐标分量的导数,得到:
\[\begin{aligned} \left.\frac{\partial}{\partial x}\right|_{q_0}\left(\chi_M * \tilde{F}\right) & =\left.\frac{\partial}{\partial x}\right|_{q=q_0} \int_{M} \tilde{F}(q-p)\mathrm{d} p\\ &=\int_{M} \left.\frac{\partial}{\partial x}\right|_{q=q_0} \tilde{F}(q-p)\mathrm{d} p\\ & =\int_{M}\left(-\frac{\partial}{\partial x} \tilde{F}\left(q_0-p\right)\right) \mathrm{d} p \\ & =-\int_{M} \nabla \cdot\left(\tilde{F}\left(q_0-p\right), 0,0\right) \mathrm{d} p\\ & =\int_{\partial M}\left\langle\left(\tilde{F}_p\left(q_0\right), 0,0\right), \vec{N}_{\partial M}(p)\right\rangle \mathrm{d} p . \end{aligned}\]这里最后一步使用了散度定理
\[\int_{M} \nabla \cdot \vec{G} \mathrm{d} p=\int_{\partial M} \left\langle \vec{G}, \vec{N}_{\partial M}(p)\right\rangle \mathrm{d} p\]同理,可以计算出关于$y$和$z$坐标分量的导数,得到:
\[\begin{aligned} \left.\frac{\partial}{\partial y}\right|_{q_0}\left(\chi_M * \tilde{F}\right) & =\int_{\partial M}\left\langle\left(0, \tilde{F}_p\left(q_0\right),0\right), \vec{N}_{\partial M}(p)\right\rangle \mathrm{d} p \\ \left.\frac{\partial}{\partial z}\right|_{q_0}\left(\chi_M * \tilde{F}\right) & =\int_{\partial M}\left\langle\left(0, 0, \tilde{F}_p\left(q_0\right)\right), \vec{N}_{\partial M}(p)\right\rangle \mathrm{d} p \end{aligned}\]将上述三个方程组合起来,得到:
\[\nabla \left( \chi_M * \tilde{F} \right) (q_0)=\int_{\partial M} \tilde{F}_p\left(q_0\right) \vec{N}_{\partial M}(p) \mathrm{d} p\]